二項分布

【Python統計学】二項分布

二項分布 (Binomial Distribution)とは、結果が二択となる試行を繰り返して、ある事象（出来事）がどのくらい発生するかを表す確率分布です。たとえば、引き分けのない試合が $10$ 回行われたとき、$7$ 勝できる確率はどのくらいかを表します。

二項試行のシミュレーション

これから「コインを $5$ 回投げて、それぞれの回で表と裏のどちらが出たかを記録する試行」を $1$ セットとする実験を $1000$ セット行なうことにします。ただし、実際にコインを投げるのではなく、乱数生成関数によるシミュレーション (仮想実験) です。
 
最初に準備として必要なモジュールをインポートして、配列の表示形式を設定しておきます。

# BINOMIAL DISTRIBUTION SIMULATION (COIN)

# In[1]

import numpy as np
import matplotlib.pyplot as plt

# 小数点以下3桁まで表示
# 10要素を超える配列は省略表示(先頭と末尾に5要素を表示)
np.set_printoptions(precision=3, threshold=10, edgeitems=5)

いま、コインの表と裏をそれぞれ 1, 0 で表すことにします。たとえば、あるセットの結果が一次元配列 [0 1 1 0 1] と表されるとき、[裏 表 表 裏 表] であったことを意味します。このような配列を $1000$ 個格納した二次元配列を numpy.random.randint() を使って生成します。

# In[2]

np.random.seed(0)

# コインを5回投げて表(1)と裏(0)を記録
# 1000セットの標本を作成
sample = np.random.randint(0, 2, (1000, 5))

print(sample)
'''
[[0 1 1 0 1]
 [1 1 1 1 1]
 [1 0 0 1 0]
 [0 0 0 0 1]
 [0 1 1 0 0]
 ...
 [1 0 0 1 0]
 [1 0 1 0 0]
 [1 0 0 1 0]
 [0 0 0 0 1]
 [1 1 1 1 1]]
'''

実行結果は省略表示されていますが、実際には $1000$ 行のデータです。この配列の列方向 (右方向) にカウントすれば、各セットで表が出た枚数が得られます。

# In[3]

# セットごとに表(head)の枚数をカウント
heads = np.count_nonzero(sample, axis=1)

print(heads)
# [3 5 2 1 2 ... 2 2 2 1 5]

numpy.sum() を使ってもカウントできますが、numpy.count_nonzero() を使った方が高速です。次は NumPy のマスク機能によって、表が $1$ 枚だったセットを抜き出してみます。

# In[4]

# 表が1枚だった事象を抽出
h1 = heads[heads==1]

print(h1)
# [1 1 1 1 1 ... 1 1 1 1 1]

numpy.count_nonzero() で、表が 1 枚だったセットの数を取得します。

# In[5]

# 表が1枚だったセットの数(頻度:frequency)
freq_h1 = np.count_nonzero(h1)

print(freq_h1)
# 134

この回数を全セット数 $1000$ で割ると、全体を $1$ とした場合の比率、すなわち「コインを $5$ 回投げて表が $1$ 枚である確率」の近似値 $0.134$ が得られます。

# In[6]

# 表が1枚である確率の近似計算
p1 = freq_h1 / 1000

print(p1)
# 0.134

他の枚数だったセットについても同様に計算できます。
ループ処理を使って「コインを $5$ 回投げて表が $0,\ 1,\ 2,\ 3,\ 4,\ 5$ 枚となる確率分布」を配列に入れます。numpy.count_nonzero() は 0 をカウントしないので、表が $0$ 枚となった頻度については、$1000$ から他のセット数の合計を引いて計算します。

# In[7]

# 全要素がゼロの配列を生成(頻度配列の初期値)
freq = np.zeros(6)

# 表が1,2,3,4,5枚となった頻度
for i in range(1, 6):
    freq[i] = np.count_nonzero(heads[heads==i])

# 表が0枚となった頻度
freq[0] = 1000 - np.sum(freq)

# 確率分布を計算
p = freq / 1000

print(p)
# [0.035 0.134 0.322 0.31  0.159 0.04 ]

Matplotlib を使って結果を棒グラフで表してみましょう。

# In[8]

# FigureとAxes
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_xlabel("Number of heads from 5 tosses", fontsize = 16)
ax.set_ylabel("Probability", fontsize = 16)

# 表が出た枚数
x = np.arange(0, 6)

# 棒グラフをプロット
ax.bar(x, p, edgecolor="black")

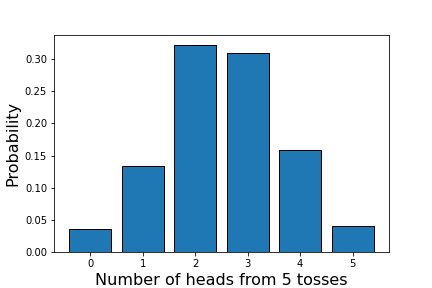
分布を見ると、左右対称 … と言えなくもない分布となっています。統計理論を使って計算すると完全に左右対称となることが知られていますが、セット数を増やすことで理論値に近づけることができます。
 
上述のコードをより一般化して、任意のセット数 s と投げるコインの数 c を入れて確率分布を返す coin_flip() 関数を定義してみます。

# In[9]

def coin_flip(s, c):
    # 標本を生成
    sample = np.random.randint(0, 2, (s, c))
    
    # 各セットの表の枚数をカウント
    heads = np.sum(sample, axis=1)
    
    # 各セットの表の枚数を格納する配列を用意
    # 初期値はすべて0
    freq = np.zeros(c+1)
    
    # 表が1枚,2枚,...,c枚の事象の数を配列に格納
    for i in range(1, c+1):
        freq[i] = np.count_nonzero(heads[heads==i])
    
    # 表が0枚の事象の数
    freq[0] = s - np.sum(freq)
    
    return freq / s

$5$ 枚のコインを投げて表が出る枚数の確率分布を、今度は $10$ 万セット (!) で計算してみます。このような途方もない実験であっても、NumPy なら一瞬で処理します。

# In[10]

# 5枚のコインを投げて表が出る枚数の確率分布
# 10万セットで計算
p = coin_flip(10**5, 5)

print(p)
# [0.032 0.155 0.313 0.313 0.157 0.031]

今回は、ほぼ左右対称な結果を得ることができました。表が 1 枚も出ないことも、$5$ 枚すべてが表であることも同じ確率で発生することは直感的に理解できます。結果をグラフにプロットしておきます。

# In[11]

# Axesをクリア
ax.cla()

# 軸の設定
ax.set_xlabel("Number of heads from 5 tosses", fontsize=16)
ax.set_ylabel("Probability", fontsize=16)

# 確率分布をプロット
ax.bar(x, p, edgecolor="black")

# Figureを再表示
display(fig)

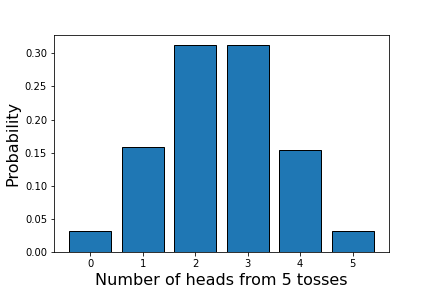
次は理論計算によって確率分布を計算してみましょう。コインを $5$ 回投げたときの、裏と表の組合わせの総数は $2^5=32$ 通りです。すべての可能性を列挙すると下図のようになります。

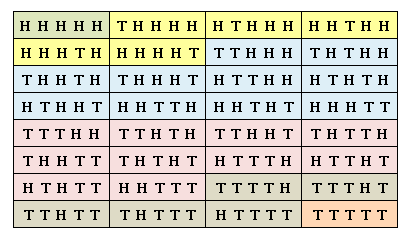
H は表 (Head)、T は裏 (Tail) を表します。
すべての事象は同じ確率 $1/2^5$ で実現します。
図は表 (裏) の枚数によって色分けしてあります。
たとえば、表が $3$ 回出る場合の数は
 \[_{5}\mathrm{C}_{3}=\frac{5!}{3!(5-3)!}=10\]
なので、表が $3$ 回出る確率は
 \[P(X=3)=\frac{_{5}\mathrm{C}_{3}}{2^5}=\frac{10}{32}=0.3125\]
となります。同様に考えて、表の出る回数 $X$ が $k$ である確率、すなわち $P(X=k)$ は
 \[P(X=k)=\frac{_{5}\mathrm{C}_{k}}{2^5}\]
によって計算できます。すべての $k$ について計算すると、
 \[\begin{align*}&P(X=0)=\frac{1}{32}=0.03125\\[6pt]&P(X=1)=\frac{5}{32}=0.15625\\[6pt]&P(X=2)=\frac{10}{32}=0.3125\\[6pt]&P(X=3)=\frac{10}{32}=0.3125\\[6pt]&P(X=4)=\frac{5}{32}=0.15625\\[6pt]&P(X=5)=\frac{1}{32}=0.03125\end{align*}\]
となります。シミュレーションの結果とも一致しています。

二項分布の期待値と分散・標準偏差

一般に $n$ 回の二項試行で事象 $A$ の起こる確率が $p$, 事象 $B$ の起こる確率が $1-p$ であるとき、事象 $A$ が $k$ 回起こる確率は
 \[P(X=k)={}_{n}\mathrm{C}_{k}\,p^{k}(1-p)^{n-k}\]
で与えられます。また、確率変数 $X$ の期待値 (平均値) と分散は
 \[\begin{align*}\mu&=np\\[6pt]\sigma^2&=np(1-p)\end{align*}\]
で与えられることが知られています (分散の平方根をとれば標準偏差 $\sigma$ を得ます)。期待値 $\mu$ は $n$ 回の二項試行で事象 $A$ が起こるおおよその回数を表します ($n$ 回の二項試行を何度も繰り返して $A$ の起こった回数を平均すれば $\mu$ に近い値が得られます)。

さきほどのコイン投げの例では、$A,\ B$ ともに $p=1/2$ の確率で生じる二項試行でしたが、$A$ と $B$ が異なる確率で生じる試行も考えられます。たとえば「サイコロを振って $1$ の目が出る事象」を $A$、「$1$ 以外の目が出る事象」を $B$ とします。$A$ が起こる確率は $p=1/6$ なので、サイコロを $10$ 回振ったときに $1$ の目が $3$ 回出る確率は
 \[P(X=3)={}_{10}\mathrm{C}_{3}\left(\frac{1}{6}\right)^{3}\left(\frac{5}{6}\right)^{7}=0.15505\]
となります。確率変数 $X$ の期待値と分散、標準偏差は、それぞれ
 \[\begin{align*}\mu&=np=10\times \frac{1}{6}=1.667\\[6pt]\sigma^2&=np(1-p)=1.389\\[6pt]\sigma&=\sqrt{\sigma^2}=1.179\end{align*}\]
となっています。すなわち、あるセットで $1$ の目が出る回数は平均して $1$ ～ $2$ 回程度で、バラつき (標準偏差) を考慮すると、$10$ セットのうち $7$ セットぐらいは $0$ ～ $4$ 回の範囲に収まるということです (標準偏差の考え方については、こちらの記事を参照してください)。

SciPy の統計分析用サブパッケージ scipy.stats から binom.pmf() をインポートすると、$P(X=k)$ の理論値を計算できます。$P(X=3)$ を求めて上の結果と一致することを確認しておきます。

# BINOMIAL DISTRIBUTION SIMULATION (DICE)

# In[1]

import numpy as np
from scipy.stats import binom

# サイコロを10回振って、1の目が3回出る確率
p3 = binom.pmf(3, 10, 1/6)

print("{:.5f}".format(p3))
# 0.15505

すべての k について $P(X=k)$ を計算すると二項分布を得ます。
分布の様子をグラフで表してみましょう。

# In[2]

import matplotlib.pyplot as plt

# FigureとAxes
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_xlabel("k", fontsize = 16)
ax.set_ylabel("P(X=k)", fontsize = 16)

# 分布を決める定数
n = 10
p = 1 / 6
k = np.arange(0, 7)

# P(X=k)を計算
pk = binom.pmf(k, n, p)

# 二項分布をプロット
ax.bar(k, pk, fc = "red", ec="black")

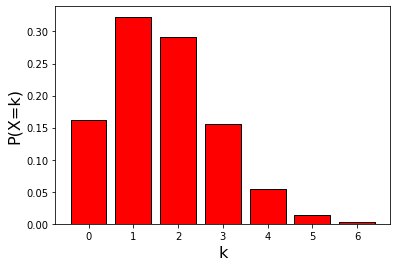
$10$ 回のうち $1$ 回だけ $1$ の目が出る確率が最も高くなっています。
確率変数 ($1$ の目が出る回数) の期待値、分散、標準偏差は、それぞれ mean(), var(), std() メソッドで取得できます。

# In[3]

# 確率変数の期待値
mu = binom.mean(n, p)

# 確率変数の分散と標準偏差
var = binom.var(n, p)
std = binom.std(n, p)

print("期待値: {:.5f}".format(mu))
print("分散: {:.5f}".format(var))
print("標準偏差: {:.5f}".format(std))

# 期待値: 1.66667
# 分散: 1.38889
# 標準偏差: 1.17851

ここでサイコロを投げる回数 $n$ を増やしていくと、二項分布についての興味深い性質を見ることができます。

# In[4]

# Axesをクリア
ax.cla()

# 軸範囲を設定
ax.set_xlim(0, 20)
#ax.set_ylim(0, 0.2)

# サイコロを投げる回数のリスト
roll = [10, 20, 30]

# プロットのカラー
c = ["red", "green", "blue"]

# ステップ数の初期値
step = -1

# 分布をプロット
for n in roll:
    step += 1
    k = np.arange(0, n+1)
    pk = binom.pmf(k, n, p)
    ax.plot(k, pk,color=c[step], marker="o", label="n={}".format(n))

# 凡例を表示
ax.legend()

# グラフを再表示
display(fig)

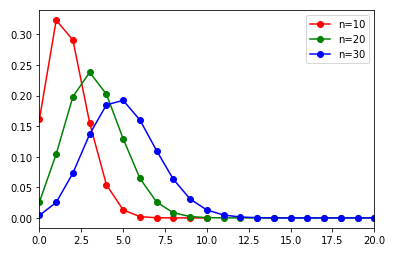
$n$ の増加にしたがって、確率変数の期待値は右へずれます。期待値の移動は $\mu=np$ から理解できますが、同時に分布の形が左右対称に近づいていることもわかります。十分に大きな $n$ をとれば、二項分布は正規分布で近似できることが知られています。

scipy.stats.binom()

SciPy の scipy.stats.binom() は二項分布オブジェクトを生成するコンストラクタです。オブジェクトの各種メソッドを用いて、確率密度関数や成功回数、平均値・分散・標準偏差などの統計値を取得できます。
 
binom.rvs(n, p) は試行 n 回のうち、成功率 p の事象の成功回数をランダムに生成します。たとえば、「サイコロを $100$ 回振って $1$ の目が出た回数を記録する」を 10 セット実行する場合は、以下のようなコードを記述します。

# SCIPY_STATS_BINOM

# In[1]

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom

# 二項分布を決める定数
n = 100
p = 1 / 6

# 試行n回のうち、確率pの事象が起こる回数
freq = binom.rvs(n, p, size=10, random_state=0)

print(freq)
# [17 19 18 17 16 18 16 21 24 15]

実行結果の平均をとれば、成功回数の期待値を得ます。
ただし、理論値ではなくシミュレーションによる近似値です。

# In[2]

# 成功数の期待値
mean = np.mean(freq)

print(mean)
# 18.1

binom.pmf(n, p) は確率密度関数の理論値を得るメソッドです。

# In[3]

# FigureとAxes
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_xlabel("k", fontsize=16)
ax.set_ylabel("P(X=k)", fontsize=16)
ax.set_xlim(0, 40)

# 成功回数
k = np.arange(0, n+1)

# P(X=k)
pk = binom.pmf(k, n, p)

# 二項分布をプロット
ax.plot(k, pk, color="blue", marker="o")

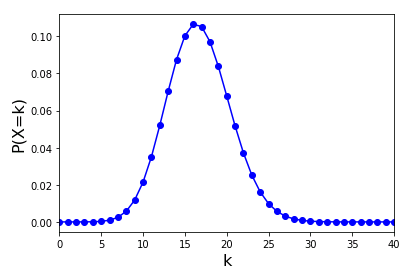
binom.median(), binom.mean(), binom.var(), binom.std() で二項分布の中央値、期待値、分散、標準偏差を取得できます。

# In[4]

# 確率変数の期待値、分散、標準偏差
mu = binom.mean(n, p)
var = binom.var(n, p)
std = binom.std(n, p)

print("期待値: {:.3f}".format(mu))
print("分散: {:.3f}".format(var))
print("標準偏差: {:.3f}".format(std))

# 期待値: 16.667
# 分散: 13.889
# 標準偏差: 3.727

numpy.random.binomial()

numpy.random.binomial(n, p, size) は二項試行を n 回行なって、確率 p で発生する事象が起こった回数を、size で指定した個数だけ返します。

NUMPY_RANDOM_BIONOMIAL

# In[1]

import numpy as np

# 省略表示の閾値を100に変更
np.set_printoptions(threshold=100)

# サイコロを10回振って1の目が出る回数
freq_d1 = np.random.binomial(10, 1/6, 100)

print(freq_d1)
# [0 2 3 2 1 1 2 1 1 1 2 1 3 1 1 0 2 2 2 1 1 0 3 2 2 0 4 2 0 1 1 0 1 4 1 0 0
#  2 0 3 2 2 0 2 2 2 1 1 3 2 0 2 2 4 2 0 0 2 3 2 1 0 1 3 3 2 5 2 1 3 1 0 3 3
#  2 2 1 0 2 0 4 4 1 3 0 2 1 1 0 1 1 3 0 1 4 1 1 2 0 0]