オイラー法
与えられた微分方程式について、通常の数学的手法を使って導き出された解を解析解(厳密解)とよびます。これまでの記事では、運動方程式の解析解を手計算で求めてからデータを作成して、結果をグラフにプロットしました。解析解は文句なしに最高精度を保証するので、一番最初に検討すべき選択肢です (与えられた微分方程式が解けるのかどうか判断に迷ったときは、SymPy に解かせてみてください)。
しかし、現実に近い状況を想定して運動方程式の右辺に色々な項が付け加えられるようになると、解析解を求めることが非常に難しくなってきます。そうした場合には、数値計算によって近似解 (数値解) を得る必要があります。幸いにも、SciPyパッケージには微分方程式を解くための高度なアルゴリズムが実装されているので、ユーザーは数値解法の手順を知らなくても精度の高い数値解を簡単に得ることができます。Python による数値シミュレーションの実践の場においては、SciPy の活用がメインとなるでしょう。
しかし、当面の間は数値解法の基礎知識を習得する目的で、オイラー法とよばれる初等アルゴリズムを実装して力学の問題を分析することを試みます。
オイラー法のアルゴリズム
$t$ の関数 $y(t)$ について、次の形の微分方程式が与えられたとします。
\[\dot{y}(t)=f(t,\ y(t))\tag{1}\]
ここで、$\dot{y}(t)$ は $y(t)$ の時間微分、つまり
\[\dot{y}(t)=\frac{dy(t)}{dt}\]
を表しています。物理学では慣用的に物理量 $f$ の時間微分を $\dot{f}$ で表すことが多いです。$\ddot{f}$ のように、文字の上に点が 2 個ついたら $f$ の二階微分を表しています。
さて、$\Delta t$ が十分に小さい値とするとき、微分の定義から左辺は次のように近似することができます。
\[\dot{y}(t)=\frac{y(t+\Delta t)-y(t)}{\Delta t}\tag{2}\]
したがって、$t$ が $t+\Delta t$ に変化したときの $y$ の値は
\[y(t+\Delta t)=y(t)+\dot{y}(t)\Delta t\tag{3}\]
で与えられます。(1) より、$\dot{y}(t)=f(t,\ y(t))$ なので、
\[y(t+\Delta t)=y(t)+f(t,y(t))\Delta t\tag{4}\]
となります。この式を使って $y$ の値を逐次求める手法を オイラー法 とよびます。たとえば、初期条件として $y(t_0)\equiv y_0$ が与えられると、以下のようにして $y$ の値を求められます。
\[\begin{align*}y(t_0+\Delta t)=y_0+f(t_0,\ y_0)\Delta t&\equiv y_1\\[6pt]y(t_0+2\Delta t)=y_1+f(t_0+\Delta t,\ y_{1}) \Delta t&\equiv y_2\\[6pt]y(t_0+3\Delta t)=y_2+f(t_0+2\Delta t,\ y_{2}) \Delta t&\equiv y_3\\[6pt]&\vdots\end{align*}\]
オイラー法で近似解を得る関数 euler_method_1ord() を実装してみましょう (末尾の 1ord は階数 1、すなわち first order の微分方程式に対応することを表しています)。実装においては、処理の高速化を図るために NumPy を活用します。
# File_Mechanics_03
# In[1]
import numpy as np
import matplotlib.pyplot as plt
# オイラー法で1階微分方程式の数値解を得る関数
# t0:tの初期値
# y0:y初期値
# tmax:tの最大値
def euler_method_1ord(t0, y0, tmax, func, n=12):
# t0~tmaxを2**n+1個に分割
t = np.linspace(t0, tmax, 2**n + 1)
# tの刻み幅⊿t
dt = t[1] - t[0]
# tと同じ形状の未初期化配列
y = np.empty_like(t)
# y[0]に初期値y0を代入
y[0] = y0
# オイラー法でt毎の数値解を計算
for k in range(len(t) - 1):
y[k+1] = y[k] + func(t[k], y[k]) * dt
return t, y
euler_method_1ord() の引数には、$t$ の初期値 t0, $y$ の初期値 y0, $t$ の最大値 tmax, 微分方程式の右辺 func, および分割指数 n を渡します。この関数は t0 ~ tmax を $2^n$ 個に分割します (このような形に分割するのは 2 進数計算と相性が良いからです)。t の刻み幅 dt は指定した n によって自動的に決まります。配列 t の各要素について y が計算されます。戻り値は t と y です。
$f(t,y(t))=y$ として、初期条件 $y(0)=1$ のもとで
\[\dot{y}(t)=y\tag{5}\]
をオイラー法で解いてみます。
# In[2]
# 微分方程式の右辺を定義
def f(t, y):
return y
# 初期条件y(0)=1でy'=yを解く
t, y = euler_method_1ord(0, 1, 5, f, n=20)
# FigureとAxes
fig, ax = plt.subplots(figsize=(6.5, 4))
ax.set_title("Solution of y' = y (Euler method)", fontsize=16, pad=10)
ax.grid()
ax.set_xlim(0, max(t))
ax.set_ylim(0, max(y))
ax.set_xlabel("t", fontsize=14, labelpad=8)
ax.set_ylabel("y", fontsize=14, labelpad=8)
# オイラー法で得た数値解をプロット
ax.plot(t, y, color="blue")
plt.show()
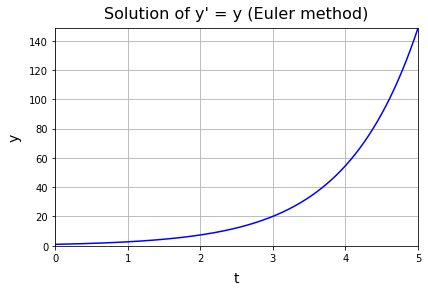
よく知られているように、微分方程式 (5) の解析解は指数関数 $y=e^t$ です。
オイラー法で得た $y(t=5)$ を numpy.exp(5) と比較してみます。
numpy.exp() は精度の高い関数なので、ほぼ真値であると考えてください。
# In[3]
print("オイラー法で得たy(5): {:.3f}".format(max(y)))
print("numpy.exp(5): {:.3f}".format(np.exp(5)))
# オイラー法で得たy(5): 148.411
# numpy.exp(5): 148.413
一般にオイラー法は収束が遅い (高い精度の解を得るために刻み幅 dt を非常に小さくする必要がある) ので、実践的な数値計算ではもっと効率的なアルゴリズムを採用すべきですが、計算原理と実装が簡単なので、当講座では、しばらくの間はオイラー法を使うことにします。
オイラー法による運動方程式の解法
古典力学では、
\[\ddot{y}(t)=f(t,y,\dot{y})\tag{6}\]
の形 (あるいはもっと簡単な形) の 2 階微分方程式をよく扱います。$t$ は時間、$y$ は物体の位置を表します。方程式 (6) をオイラー法で解いてみましょう。$v(t)=\dot{y}(t)$ とおくと、(6) は
\[\dot{v}(t)=f(t,y,\dot{y})\tag{7}\]
と表せます。微小な $\Delta t$ について
\[\frac{v(t+\Delta t)-v(t)}{\Delta t}=f(t,y,\dot{y})\tag{8}\]
が成り立つので、
\[v(t+\Delta t)=v(t)+f(t,y,\dot{y})\Delta t\tag{9}\]
となります。$v(t)=\dot{y}(t)$ は
\[y(t+\Delta t)=y(t)+v(t)\Delta t\tag{10}\]
と表せるので、(9) で計算した $v(t)$ を (10) に代入して $y(t)$ を得ることができます。
オイラー法で 2 階微分方程式を解く関数 euler_method_2ord() を実装してみましょう。
# In[4]
# オイラー法で2階微分方程式の数値解を得る関数
# t0:tの初期値
# v0:vの初期値
# y0:y初期値
# tmax:tの最大値
def euler_method_2ord(t0, v0, y0, tmax, func, n=12):
# t0~tmaxを2**n+1個に分割
t = np.linspace(t0, tmax, 2**n + 1)
# tの刻み幅⊿t
dt = t[1] - t[0]
# tと同じ形状の未初期化配列を生成
v = np.empty_like(t)
y = np.empty_like(t)
# v[0]に初期値y0を代入
v[0] = v0
y[0] = y0
# オイラー法でt毎の数値解を計算
for k in range(len(t) - 1):
v[k+1] = v[k] + func(t[k], y[k], v[k]) * dt
y[k+1] = y[k] + v[k] * dt
return t, v, y
月の上空 $100$ m の高さから初速度 $0$ で自由落下させた物体の運動方程式
\[\ddot{y}=-g\tag{11}\]
をオイラー法で解いてみましょう。
# In[5]
# 運動方程式の右辺を設定
def f(t, y, v):
g = 1.62
return -g
# オイラー法でy''=-gを解く
t, v, y = euler_method_2ord(0, 0, 100, 12, f, n=16)
# FigureとAxesの設定
fig, ax = plt.subplots(2, 1, figsize=(6, 8), sharex="col",
gridspec_kw=dict(hspace=0.25))
# 速度の時間変化をプロット
ax[0].set_title("Velocity vs time", fontsize=14, pad=10)
ax[0].grid()
ax[0].set_xlim(0, max(t))
ax[0].set_ylim(min(v), 0)
ax[0].set_ylabel("v [m/s]", fontsize=14, labelpad=8)
ax[0].plot(t, v, color="blue")
# 高度の時間変化をプロット
ax[1].set_title("Position vs time", fontsize=14, pad=10)
ax[1].grid()
ax[1].set_xlim(0, max(t))
ax[1].set_ylim(0, max(y))
ax[1].set_xlabel("t [s]", fontsize=14, labelpad=8)
ax[1].set_ylabel("y [m]", fontsize=14, labelpad=8)
ax[1].plot(t, y, color="red",
label="numerical solution")
# 下のグラフに解析解を重ねる
y2 = 100 - (1.62 * t**2) / 2
ax[1].plot(t, y2, linestyle="--", color="black",
label="analytical solution")
# 凡例を表示
ax[1].legend()
plt.show()
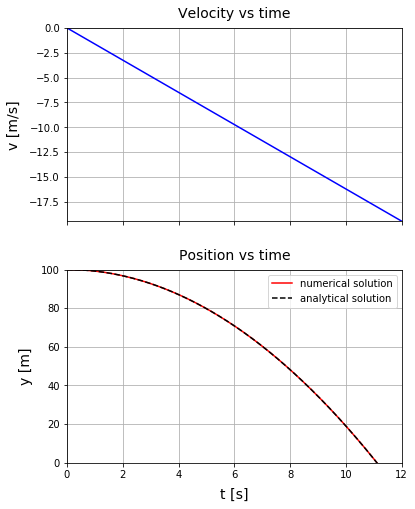
月面から鉛直上向きに $y$ 軸をとっているので、速度は負の値をとります。
Position vs time のグラフから、上空 $100$ m の高さから落下する物体は約 $11$ 秒後に月面に衝突することがわかります。黒い点線で解析解も表示していますが、きれいに数値解と重なっています。
コメント
オイラー法を使えば右辺には関数に限らず、観測データをプロットしたグラフであっても t 軸との間の(短冊の寄せ集めとしての)面積を計算することができるという理解でいいのでしょうか。
時間 t に依存する物理量 A(t) の時間変化が
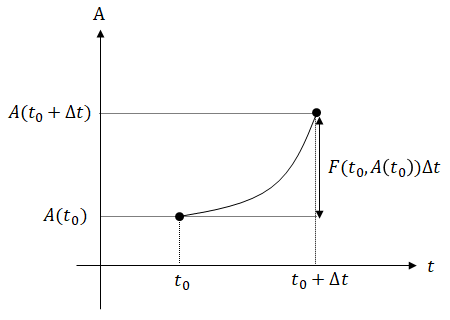
dA(t)/dt = F(t, A(t))
の形で与えられるとします。物理学においては、一般に右辺は物体に継続的に加えられる力 (重力、電場から受ける力、摩擦力など) だと考えてください。上の表式では、力 F は時刻 t と、そのときの物理量 A(t) に依存します(重力や摩擦力のような単純な力の場合、どの t でも F は一定値をとると考えます)。オイラー法は、時刻 t0 から微小時間 Δt だけ経過したときの物理量 A(t0 + Δt) が、時刻 t0 の時の力 F(t0, A(t0)) を使って、
A(t0 + Δt) = A(t0) + F(t0, A(t0))Δt
のように近似できるというものです。このとき、物理量 A(t) の時間変化は下図のようになります。
おっしゃるように、F は観測されるデータであっても構いません。たとえば、荷電粒子にはたらく電場の形を刻一刻と変化させるような状況が考えられます。もともと右辺に何か関数が与えられたとしても、数値計算上はそれを離散データにして配列に格納するので同じことです。
たいへん丁寧なご回答をありがとうございました。
dA(t)/dt=F(t, A(t)) において、A(t)がどんな関数からわからないのに、初期値から積み上げて計算するだけで近似値が得られるのは少し不思議な感じがしました。
下記は誤植と思われますので、ご確認ください。
In[5] プログラムのコメントで、y ‘ ‘ =-mg → y ‘ ‘ = -g
ありがとうございます。修正しておきました。