線形基底関数モデル

線形基底関数モデル

前回までは 25歳以下に限定した年齢と体重のデータを使っていました。今回は年齢制限をなくして、幅広い年齢層から 20人を無作為抽出したデータを使用します。

# Linear_basis_function_models

# In[1]

import numpy as np
import matplotlib.pyplot as plt

# 配列の表示設定
np.set_printoptions(precision=3, floatmode="fixed")

# 20人の年齢と体重のデータセット
x = np.array([35, 16, 22, 43, 5,
              66, 20, 13, 52, 1,
              39, 62, 45, 33, 8,
              28, 71, 24, 18, 3])

y = np.array([85.19, 58.93, 64.27, 68.91, 21.27,
              68.88, 60.07, 55.18, 88.08, 8.89,
              82.31, 81.18, 80.76, 78.98, 37.55,
              75.9, 72.39, 69.51, 62.04, 12.47])

まずは与えられたデータをプロットしてみます。

# In[2]

# FigureとAxesの設定
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111)
ax.set_title("Age vs. Weight", fontsize=16)
ax.grid()
ax.set_xlim([0, 70])
ax.set_ylim([0, 100])
ax.set_xlabel("Age", fontsize=14)
ax.set_ylabel("Weight [kg]", fontsize=14)

# 身長と体重データの散布図
ax.scatter(x, y, color="blue")

plt.show()

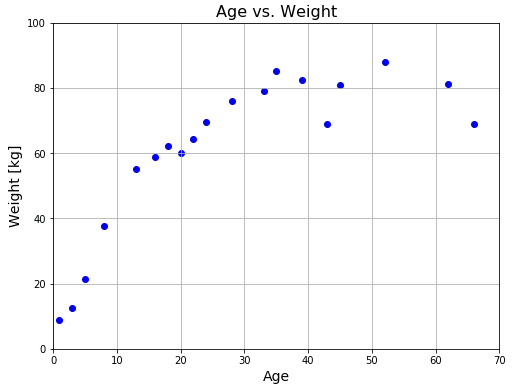
このグラフを直線で近似するのは明らかに無理があります。人間の身体的成長には限界があるので、ある年齢で体重の増加が頭打ちになることは常識的観点からもわかります。そこで、上のグラフを近似できるような別の関数を探すことにします。

基底関数モデル

とはいえ、「どのような関数をもってくればデータにフィットさせることができるのか」を判断することは難しいので、いくつかの関数を組合わせて近似曲線をつくることを考えます。すなわち、基底関数とよばれる $M$ 個の関数のセット
 $${\varphi }_0(x),{\varphi }_1(x),\dots {\varphi }_{M-1}(x)$$
を用意して、各関数に重みをつけて足し合わせ、
 $$\begin{array}{}\text{(１)}& f(x)=a_0{\varphi }_0(x)+a_1{\varphi }_1(x)+a_2{\varphi }_2(x)+\cdots +a_{M-1}{\varphi }_{M-1}(x)+a_M\end{array}$$
という関数を近似関数とします。基底関数の選択に関しては、扱う問題ごとにプログラマーに委ねられますが、判断しにくい場合は多項式や ガウス関数 などの汎用性の高い関数を与えておきます。係数 $a_k$ は基底関数の重みとよばれるパラメータで、こちらは最小二乗法のアルゴリズムにしたがって計算機のほうで調整してくれます。うまくフィットしない場合は、基底関数の種類や数を変えて再計算させるなど、ある程度の試行錯誤は必要です。

パラメータ $a_k$ の求め方は前回と同じです。次のような $N$ 個の入力データ $\mathit{x}$ と目標データ $\mathit{y}$ が与えられたとします。
 $$\begin{array}{}\text{(2)}& \mathit{x}=\left[\begin{array}{c}{x}_0\\ x_1\\ ⋮\\ x_{N-1}\end{array}\right],\mathit{y}=\left[\begin{array}{c}{y}_0\\ y_1\\ ⋮\\ y_{N-1}\end{array}\right]\end{array}$$
ここでは記述を簡単にするために、$2$ つの基底関数を用いて
 $$\begin{array}{}\text{(3)}& f(x)=a_0{\varphi }_0(x)+a_1{\varphi }_1(x)+a_2\end{array}$$
という関数を用意します。常に $1$ をとるような $3$ つめの基底関数 ${\varphi }_2(x)$ を定義すると、
 $$\begin{array}{}\text{(4)}& f(x)=a_0{\varphi }_0(x)+a_1{\varphi }_1(x)+a_2{\varphi }_2(x)\end{array}$$
と表すことができます。入力データベクトルに対しては、
 $$\begin{array}{}\text{(5)}& \mathit{f}(\mathit{x})=a_0\left[\begin{array}{c}{\varphi }_0(x_0)\\ {\varphi }_0(x_1)\\ ⋮\\ {\varphi }_0(x_{N-1})\end{array}\right]+a_1\left[\begin{array}{c}{\varphi }_1(x_0)\\ {\varphi }_1(x_1)\\ ⋮\\ {\varphi }_1(x_{N-1})\end{array}\right]+a_2\left[\begin{array}{c}{\varphi }_2(x_0)\\ {\varphi }_2(x_1)\\ ⋮\\ {\varphi }_2(x_{N-1})\end{array}\right]\end{array}$$
となります。ここで、
 $$\begin{array}{}\text{(6)}& {\mathit{\varphi }}_{\mathbf{0}}=\left[\begin{array}{c}{\varphi }_0(x_0)\\ {\varphi }_0(x_1)\\ ⋮\\ {\varphi }_0(x_{N-1})\end{array}\right],{\mathit{\varphi }}_{\mathbf{1}}=\left[\begin{array}{c}{\varphi }_1(x_0)\\ {\varphi }_1(x_1)\\ ⋮\\ {\varphi }_1(x_{N-1})\end{array}\right],{\mathit{\varphi }}_{\mathbf{2}}=\left[\begin{array}{c}{\varphi }_2(x_0)\\ {\varphi }_2(x_1)\\ ⋮\\ {\varphi }_2(x_{N-1})\end{array}\right]=\left[\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right]\end{array}$$
というベクトルを定義すると、
 $$\begin{array}{}\text{(7)}& \mathit{f}(\mathit{x})=a_0{\mathit{\varphi }}_{\mathbf{0}}+a_1{\mathit{\varphi }}_{\mathbf{1}}+a_2{\mathit{\varphi }}_{\mathbf{2}}\end{array}$$
と表せます。$\mathit{f}(\mathit{x})$ と実際の目標データ $\mathit{y}$ の差の平方、
 $$\begin{array}{}\text{(8)}& |\mathit{y}-\mathit{f}(\mathit{x}){|}^2=|\mathit{y}-(a_0{\mathit{\varphi }}_{\mathbf{0}}+a_1{\mathit{\varphi }}_{\mathbf{1}}+a_2{\mathit{\varphi }}_{\mathbf{2}}){|}^2\end{array}$$
を最小にするようにパラメータ $a_k$ を決めます。$a_0{\mathit{\varphi }}_{\mathbf{0}}+a_1{\mathit{\varphi }}_{\mathbf{1}}+a_2{\mathit{\varphi }}_{\mathbf{2}}$ は $N$次元空間内で ${\mathit{\varphi }}_{\mathbf{0}},{\mathit{\varphi }}_{\mathbf{1}},{\mathit{\varphi }}_{\mathbf{2}}$ の 3本のベクトルが張る空間内 $V$ を動くベクトルです。この点を $\mathrm{P}$ とおきます。$\mathit{y}$ は $N$次元空間内の固定された点です。この点を $\mathrm{Q}$ とおくと、
 $$\begin{array}{}\text{(9)}& \overrightarrow{\mathrm{PQ}}=\mathit{y}-(a_0{\mathit{\varphi }}_{\mathbf{0}}+a_1{\mathit{\varphi }}_{\mathbf{1}}+a_2{\mathit{\varphi }}_{\mathbf{2}})\end{array}$$
となります。$|\overrightarrow{\mathrm{PQ}}|$ が最小となるような点 $\mathrm{P}$ は、$\mathrm{Q}$ から 空間 $V$ に下ろした垂線の足 $\mathrm{H}$ と一致します。空間に下ろす垂線をイメージするのは難しいですが、要するに $\overrightarrow{\mathrm{PQ}}$ は ${\mathit{\varphi }}_{\mathbf{0}},{\mathit{\varphi }}_{\mathbf{1}},{\mathit{\varphi }}_{\mathbf{2}}$ の 3本のベクトルと内積をとると、いずれも $0$ になるということです。
 $$\begin{array}{}\text{(10)}& \begin{array}{r}(\mathit{y}-a_0{\mathit{\varphi }}_{\mathbf{0}}-a_1{\mathit{\varphi }}_{\mathbf{1}}-a_0{\mathit{\varphi }}_{\mathbf{2}})\cdot {\mathit{\varphi }}_{\mathbf{0}}=0\\ (\mathit{y}-a_0{\mathit{\varphi }}_{\mathbf{0}}-a_1{\mathit{\varphi }}_{\mathbf{1}}-a_0{\mathit{\varphi }}_{\mathbf{2}})\cdot {\mathit{\varphi }}_{\mathbf{1}}=0\\ (\mathit{y}-a_0{\mathit{\varphi }}_{\mathbf{0}}-a_1{\mathit{\varphi }}_{\mathbf{1}}-a_0{\mathit{\varphi }}_{\mathbf{2}})\cdot {\mathit{\varphi }}_{\mathbf{2}}=0\end{array}\end{array}$$
これを行列形式で書き直すと次のようになります。
 
$$\begin{array}{}\text{(11)}& \left[\begin{array}{ccc}{\mathit{\varphi }}_{\mathbf{0}}\cdot {\mathit{\varphi }}_{\mathbf{0}}& {\mathit{\varphi }}_{\mathbf{1}}\cdot {\mathit{\varphi }}_{\mathbf{0}}& {\mathit{\varphi }}_{\mathbf{2}}\cdot {\mathit{\varphi }}_{\mathbf{0}}\\ {\mathit{\varphi }}_{\mathbf{0}}\cdot {\mathit{\varphi }}_{\mathbf{1}}& {\mathit{\varphi }}_{\mathbf{1}}\cdot {\mathit{\varphi }}_{\mathbf{1}}& {\mathit{\varphi }}_{\mathbf{2}}\cdot {\mathit{\varphi }}_{\mathbf{1}}\\ {\mathit{\varphi }}_{\mathbf{0}}\cdot {\mathit{\varphi }}_{\mathbf{2}}& {\mathit{\varphi }}_{\mathbf{1}}\cdot {\mathit{\varphi }}_{\mathbf{2}}& {\mathit{\varphi }}_{\mathbf{2}}\cdot {\mathit{\varphi }}_{\mathbf{2}}\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\end{array}\right]=\left[\begin{array}{c}\mathit{y}\cdot {\mathit{\varphi }}_{\mathbf{0}}\\ \mathit{y}\cdot {\mathit{\varphi }}_{\mathbf{1}}\\ \mathit{y}\cdot {\mathit{\varphi }}_{\mathbf{2}}\end{array}\right]\end{array}$$
記述を簡単にするために $N=3$ とします（一般の $N$ でも以下の変形手順は同じです）。
基底関数行列 $\mathrm{\Phi }$ とパラメータベクトル $\mathit{p}$ を
 $$\begin{array}{}\text{(12)}& \mathrm{\Phi }=\left[\begin{array}{ccc}{\varphi }_0(x_0)& {\varphi }_1(x_0)& {\varphi }_2(x_0)\\ {\varphi }_0(x_1)& {\varphi }_1(x_1)& {\varphi }_2(x_1)\\ {\varphi }_0(x_2)& {\varphi }_1(x_2)& {\varphi }_2(x_2)\end{array}\right],\mathit{p}=\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\end{array}\right]\end{array}$$
のように定義すると、式 (11) は
 $$\begin{array}{}\text{(13)}& {\mathrm{\Phi }}^T\mathrm{\Phi }\mathit{p}={\mathrm{\Phi }}^T\mathit{y}\end{array}$$
と表すことができます。両辺に左側から ${\mathrm{\Phi }}^T\mathrm{\Phi }$ の逆行列をかけると
 $$\begin{array}{}\text{(14)}& \mathit{p}=({\mathrm{\Phi }}^T\mathrm{\Phi }{)}^{-1}{\mathrm{\Phi }}^T\mathit{y}\end{array}$$
となります。$({\mathrm{\Phi }}^T\mathrm{\Phi }{)}^{-1}{\mathrm{\Phi }}^T$ は前回記事でも現れた疑似逆行列（一般化逆行列）です。

多項式近似

曲線を $x$ の $n$ 次式で近似することを多項式近似とよびます。前回までは $x$ の $1$ 次式で近似していたので、線形回帰も多項式近似に含まれます。今回は曲線を $2$ 次式で近似することを試みます。すなわち基底関数として
 $$\begin{array}{}\text{(15)}& {\varphi }_0(x)=x^2,{\varphi }_1(x)=x\end{array}$$
を選んで、データを二次関数
 $$\begin{array}{}\text{(16)}& a{x}^2+bx+c\end{array}$$
で近似するようなパラメータ $a,b,c$ を決定します。

# In[3]

# 疑似逆行列関数
def pseudo_inverse(x):
    return np.linalg.inv(x.T @ x) @ x.T

# φ0とφ1の設定
def phi_0(x):
    return x ** 2

def phi_1(x):
    return x

# 基底関数行列Φ
Phi = np.array([phi_0(x), phi_1(x), np.ones(len(x))]).T

# Φの疑似逆行列を求める
pi_Phi = pseudo_inverse(Phi)

# パラメータベクトルの決定
p = pi_Phi @ y

# 近似曲線の係数を表示
print("p = {}".format(p))

# 平均2乗誤差mseを計算
fx = p[0]*x**2 + p[1]*x + p[2]
mse = np.mean((fx-y)**2)

# 標準偏差SDを表示
print("SD = {0:.2f} kg".format(np.sqrt(mse)))

# FigureとAxesの設定
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111)
ax.set_title("Age vs. Weight", fontsize=16)
ax.grid()
ax.set_xlim([0, 70])
ax.set_ylim([0, 100])
ax.set_xlabel("Age", fontsize=14)
ax.set_ylabel("Weight [kg]", fontsize=14)

# 身長と体重データの散布図
ax.scatter(x, y, color="blue")

# 近似曲線の描画
x2 = np.linspace(0, 70, 100)
y2 = p[0]*x2**2 + p[1]*x2 + p[2]
ax.plot(x2, y2, color="red")

plt.show()
# p = [-0.0343  3.2275 10.0832]
# SD = 5.68 kg

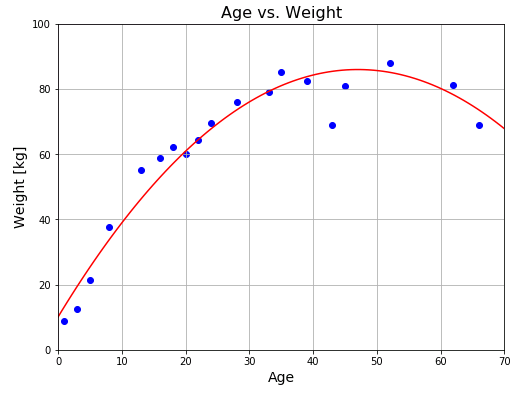
標準偏差 SD はフィッティング精度を示す値で、この値が大きいほど実際のデータと近似曲線のずれが大きいことを意味します。多項式近似からは少し離れてしまいますが、3 つめの基底関数として対数関数 $\log x$ を加えてみると、もう少しだけ精度が上がります。

# In[4]

# 3つめの基底関数
def phi_2(x):
    return np.log(x)

# 基底関数行列Φ
Phi = np.array([phi_0(x), phi_1(x), phi_2(x), np.ones(len(x))]).T

# Φの疑似逆行列
pi_Phi = pseudo_inverse(Phi)

# パラメータベクトルの決定
p = pi_Phi @ y

# 係数を表示
print("p = {}".format(p))

# 平均2乗誤差mseを計算
fx = p[0] * phi_0(x) + p[1] * phi_1(x) + p[2] * phi_2(x) + p[3]
mse = np.mean((fx-y)**2)

# 標準偏差SDを表示
print("SD = {0:.2f} kg".format(np.sqrt(mse)))

# FigureとAxesの設定
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111)
ax.set_title("Age vs. Weight", fontsize=16)
ax.grid()
ax.set_xlim([0, 70])
ax.set_ylim([0, 100])
ax.set_xlabel("Age", fontsize=14)
ax.set_ylabel("Weight [kg]", fontsize=14)

# 身長と体重データの散布図
ax.scatter(x, y, color="blue")

# 近似曲線を描画
x2 = np.linspace(1, 70, 100)
y2 = p[0] * phi_0(x2) + p[1] * phi_1(x2) + p[2] * phi_2(x2) + p[3]
ax.plot(x2, y2, color="red")

plt.show()
# p = [-0.0243  2.0948  9.5511  2.0261]
# SD = 4.90 kg

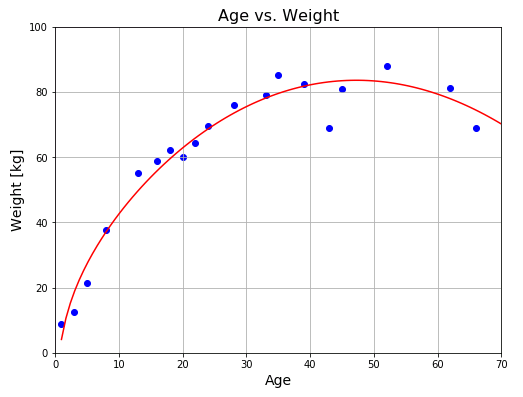
基底関数の組合わせ方は無数にあるので、最適な近似関数を見つけることは事実上不可能ですが、今後の記事でオーバーフィッテングの問題と絡めて、より良いモデルを選択する方法（ベストではなくベターなモデルに改良していく方法）について解説していく予定です。