【Pythonで学ぶ線形代数学講座(10)】行列の加算と減算・行列積
行列の定義と演算規則
連立一次方程式 について簡単に復習しておきましょう。次のような方程式を解いてみます。
\[\begin{align*}&5x-y=9\tag{1}\\[6pt]&2x+3y=7\tag{2}\end{align*}\]
$x$ と $y$ の 2 つの未知数があるので、このうち 1 つを消去することを考えます。ここでは $y$ を消去することにします。(2) はそのままにして、(1) の両辺に 3 を掛けます。
\[\begin{align*}&15x-3y=27\tag{3}\\[6pt]&2x+3y=7\tag{4}\end{align*}\]
$y$ の係数が揃いました。(3) と (4) の両辺を加えると $3y$ の項が消えます。
\[17x=34\tag{5}\]
両辺を $17$ で割ると $x=2$ を得ます。これを元の方程式の (1) に代入して
\[10-y=9\tag{6}\]
これを解いて $y=1$ を得ます。
未知数が増えたりすると、もっと手数がかかりますが、未知数にかかる係数をあれこれ操作していけば、いずれは方程式の解が現れます。方程式の見た目の違いによらず、解を求めるための一般的な係数操作を見つけることが線形代数の目的の1つです。
行列とベクトルの積
一般的な二元一次連立方程式
\[\begin{align*}&ax+by=p\tag{7}\\[6pt]&cx+dy=q\tag{8}\end{align*}\]
について考えます。左辺の係数をすべて分離して次のように表すことにします。
\[\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}p\\q\end{bmatrix}\tag{9}\]
$\begin{bmatrix}x\\y\end{bmatrix}$ と $\begin{bmatrix}p\\q\end{bmatrix}$ をベクトルと考えて、それぞれ $\boldsymbol{x},\ \boldsymbol{p}$ で表すことにします。
係数を集めたグループ $\begin{bmatrix}a&b\\c&d\end{bmatrix}$ を 2 行 2 列の 行列 とよび、$A$ で表すことにすると、(9) は
\[A\boldsymbol{x}=\boldsymbol{p}\tag{10}\]
と書けます。(9) は (7),(8) に対応しているので、行列 $A$ はベクトル $\boldsymbol{x}$ に対して
\[\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}ax+by\\cx+dy\end{bmatrix}\tag{11}\]
という演算を行なっていることになります。この演算を 行列とベクトルの積 と定義します。

行列はベクトルを別のベクトルに変換します。
このような形式の変換を 線形変換 とよびます。冒頭で扱った連立方程式
\[\begin{align*}5x-y=9\tag{1}\\[6pt]2x+3y=7\tag{2}\end{align*}\]
を行列を使って表すと、
\[\begin{bmatrix}5&-1\\2&3\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}
=\begin{bmatrix}9\\7\end{bmatrix}\tag{12}\]
となります。この連立方程式を解くことは、行列 $\begin{bmatrix}5&-1\\2&3\end{bmatrix}$ によってベクトル $\begin{bmatrix}9\\7\end{bmatrix}$ に変換されるようなベクトル $\begin{bmatrix}x\\y\end{bmatrix}$ を見つけ出すということです。
今の段階では、まだ行列によって連立方程式を解く手順を知りませんが、先ほど普通の方法で解 $x=2,\ y=1$ を得ているので、行列 $\begin{bmatrix}5&-1\\2&3\end{bmatrix}$ によってベクトル $\begin{bmatrix}2\\1\end{bmatrix}$ がベクトル $\begin{bmatrix}9\\7\end{bmatrix}$ に変換されることを確認しておきます。
\[\begin{bmatrix}5&-1\\2&3\end{bmatrix}\begin{bmatrix}2\\1\end{bmatrix}=\begin{bmatrix}5\times 2+(-1)\times 1\\2\times 2+3\times 1\end{bmatrix}=\begin{bmatrix}9\\7\end{bmatrix}\]
NumPy で行列とベクトルの積を計算するときは、numpy.dot() 関数を使います (以前の記事では引数にベクトルを 2 つ渡して内積を計算しました)。
# numpy_matrix_vector_product
# In[1]
import numpy as np
# 2×2行列を定義
A = np.array([[5, -1],
[2, 3]])
# ベクトルを定義
x = np.array([2, 1])
# 行列とベクトルの積を計算
Ax = np.dot(A, x)
print(Ax)
# [9 7]
線形変換の意味
それでは、行列による変換とは具体的にどのような変換を表しているのでしょうか。式 (12) の左辺を計算すると
\[\begin{bmatrix}5&-1\\2&3\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}5x-y\\2x+3y\end{bmatrix}\tag{13}\]
となりますが、このベクトルは次のように変形することができます。
\[\begin{bmatrix}5x-y\\2x+3y\end{bmatrix}=x\begin{bmatrix}5\\2\end{bmatrix}+y\begin{bmatrix}-1\\3\end{bmatrix}\tag{14}\]
右辺はベクトル $\begin{bmatrix}5\\2\end{bmatrix}$ と $\begin{bmatrix}-1\\3\end{bmatrix}$ の線形結合を表しています。つまり、連立方程式 (1), (2) は基底 $\begin{bmatrix}5\\2\end{bmatrix}$ と $\begin{bmatrix}-1\\3\end{bmatrix}$ を使ってベクトル $\begin{bmatrix}9\\7\end{bmatrix}$ にぴったり一致するように $x$ と $y$ を決める問題であることを意味しています(下図参照)。
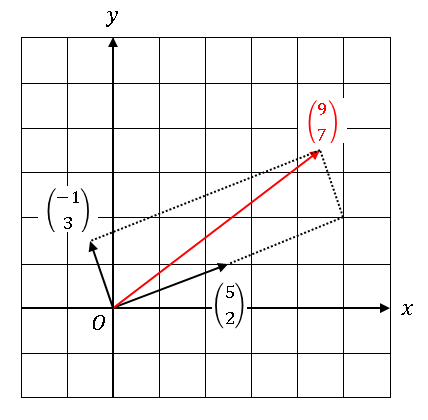
(1), (2) は簡単な問題なので、図を正しく描けば解を求めることができます。もう少し複雑な問題であっても、2 次元であれば、解がおおよそどのぐらいの値をとるのか見当をつけることはできます。
以上の考察から、行列 $A=\begin{bmatrix}a&b\\c&d\end{bmatrix}$ は縦ベクトルを横に並べたものだと考えることができます。
\[A=\begin{bmatrix}a&b\\c&d\end{bmatrix}=\begin{bmatrix}\begin{bmatrix}a\\c\end{bmatrix}&\begin{bmatrix}b\\d\end{bmatrix}\end{bmatrix}\tag{15}\]
実は行列を横ベクトルを縦に並べたものと考えることもできるのですが、それについてはまた別の機会に解説します。NumPy の配列も 2 次元配列 (行列) の中に 1 次元配列 (ベクトル) を格納するという構造になっています。
行列の和と差
行列をベクトルを並べて作られるものと考えるならば、行列の和と差について、複数のベクトルの和(あるいは差)をまとめて処理するように定義するのが自然です。
\[\begin{bmatrix}a&b\\c&d\end{bmatrix}\pm\begin{bmatrix}e&f\\g&h\end{bmatrix}=\begin{bmatrix}a\pm e&b\pm f\\c\pm g&d\pm h\end{bmatrix}\tag{16}\]
このルールは一般の $m\times n$ 行列にそのまま拡張できまます。
たとえば、$2\times 3$ の行列同士の和と差は
\[\begin{bmatrix}a_1&b_1&c_1\\d_1&e_1&f_1\end{bmatrix}\pm\begin{bmatrix}a_2&b_2&c_2\\d_2&e_2&f_2\end{bmatrix}=\begin{bmatrix}a_1\pm a_2&b_1\pm b_2&c_1\pm c_2\\d_1\pm d_2&e_1\pm e_2&f_1\pm f_2\end{bmatrix}\]
のように計算できます。しかし、$2\times 3$ の行列に $2\times 2$ の行列を加えることはできません。つまり和と差に関しては、行列のサイズが完全に一致していなければなりません。
行列の和については、交換法則・分配法則・結合法則がすべて成り立ちます。
\[\begin{align*}&A+B=B+A\tag{17}\\[6pt]&k(A+B)=kA+kB\tag{18}\\[6pt]&A+(B+C)=A+B+C\tag{19}\end{align*}\]
行列積
行列 $A$ によるベクトル $\begin{bmatrix}p\\ q\end{bmatrix}$ と、ベクトル $\begin{bmatrix}r\\ s\end{bmatrix}$ の線形変換を考えます。
\[\begin{align*}\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}p\\ q\end{bmatrix}=\begin{bmatrix}ap+bq\\cp+dq\end{bmatrix}\\[6pt]\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}r\\ s\end{bmatrix}=\begin{bmatrix}ar+bs\\cr+ds\end{bmatrix}\end{align*}\]
行列同士の積は、この変換をまとめて処理できるように定義します。すなわち、
\[\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}p&q\\r&s\end{bmatrix}
=\begin{bmatrix}ap+bq&ar+bs\\cp+dq&cr+ds\end{bmatrix}\tag{20}\]
と定義します。
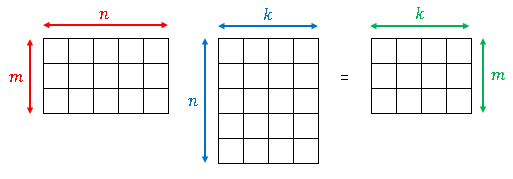
このルールをサイズの異なる行列同士の積に拡張します。
$2\times 3$ の行列の右側には $3\times k$ の行列を掛けます。
$k$ は任意の自然数です。
つまり行数が $3$ であれば列数に制限をつけません。たとえば、
\[\begin{align*}&\begin{bmatrix}a&b&c\\d&e&f\end{bmatrix}
\begin{bmatrix}g\\h\\i\end{bmatrix}=\begin{bmatrix}ag+bi+ck\\dg+ei+fk\end{bmatrix}\\[6pt]&\begin{bmatrix}a&b&c\\d&e&f\end{bmatrix}\begin{bmatrix}g&h\\i&j\\k&l\end{bmatrix}=\begin{bmatrix}ag+bi+ck&ah+bj+cl\\dg+ei+fk&dh+ej+fl\end{bmatrix}\end{align*}\]
のように計算します (ベクトルは $k\times 1$ の行列と考えます)。一般に $m\times n$ の行列の右側には $n\times k$ ($k$ は任意の自然数) の行列を掛けて、その演算結果は $m\times k$ の行列となります(下図参照)。
同じ行列 $A$ を $n$ 個掛けることを、
\[AAA\ \cdots\ A=A^n\tag{21}\]
と書いて $A$ の $n$ 乗と読みます。スカラーのべき乗と同様に、
\[(A^m)(A^n)=A^{m+n}\tag{22}\]
が成り立ちます。
行列積においては可換法則 $AB=BA$ は必ずしも成り立たない(成り立つ場合もあれば、成り立たない場合もある)ので、計算途中で積の順序をうっかり変えないように注意します。行列積の分配法則は
\[\begin{align*}C(A+B)=CA+CB\tag{23}\\[6pt](A+B)C=AC+BC\tag{24}\end{align*}\]
となります。3 つ以上の行列積 $ABC$ を計算するときに、順序さえ変えなければ、$AB$ を先に計算してから $C$ を掛けても、$BC$ を計算してから $A$ を掛けても結果は同じです。すなわち、次の結合法則
\[A(BC)=(AB)C\tag{25}\]
が成り立ちます。
numpy.dot()
numpy.dot() を使って行列積を計算できます。
# numpy_matrix_product
# In[1]
import numpy as np
a = np.array([[-1, 5],
[ 7, 0]])
b = np.array([[ 3, 1],
[-2, 6]])
# 行列積abを計算
ab = np.dot(a, b)
print(ab)
# [[-13 29]
# [ 21 7]]
numpy.linalg.multi_dot()
numpy.linalg.multi_dot() は配列のリストを受け取って行列積を返します。
# numpy_multi_matrix_product
# In[1]
import numpy as np
a = np.array([[3, 0],
[1, 2]])
b = np.array([[0, -1],
[5, 1]])
c = np.array([[ 1, 4],
[-3, 1]])
# 行列積abcを計算
abc = np.linalg.multi_dot([a, b, c])
print(abc)
# [[ 9 -3]
# [ 7 41]]

コメント
下記は誤植と思われますので、ご確認ください。
(12)式の下の行列計算で、|5 -1||9|→|5 -1||2|
|2 3||7| |2 3||1|
(16)式の下の行列計算で、|a1+a2 b1+b2 c1+c2|→|a1±a2 b1±b2 c1±c2|
|d1+d2 e1+e2 f1+f2 | |d1±d2 e1±e2 f1±f2 |
恐れ入ります m(_ _)m
直しておきました。