バックプロパゲーション

損失関数の勾配

　ニューラルネットワークは、ある層の出力値の線形結合を次の層に渡すことを繰り返すので、ネットワークからの出力ベクトル $\boldsymbol{y}$ には、入力ベクトル $\boldsymbol{x}$ と使用されたすべての重み情報が含まれることになります。損失関数 $E$ は出力値 $\boldsymbol{y}$ と正解値 $\boldsymbol{t}$ を使って計算します。ネットワークは $E$ が最小になるように重みを調整することで学習を進めます。十分に学習（訓練）を重ねたネットワークは、未知のデータが入力されたときに信頼性の高い予測値を示すことができるようになります。
　
　ネットワークに学習させるためには、使用されたすべての重み $w$ について、損失関数の偏微分 $\cfrac{\partial E}{\partial w}$ を求める必要があります。
　
　コンピュータで微分を計算する方法として、数値微分という手法が広く知られています。これは非常に小さな値 $\epsilon$ を設定して近距離にある $2$ 点の傾きを微分の近似値とする方法です。
　
\[\frac{\partial E}{\partial w}=\frac{E(w+\epsilon)-E(w-\epsilon)}{2\epsilon}\]
　しかしながら、実用的なニューラルネットワークでは、重みの総数が数百～数千、場合によっては数万というオーダーに達します。いくらコンピュータを使っていても、重み１つ１つについて数値微分で $\cfrac{\partial E}{\partial w}$ を計算するのは大変な負荷がかかります。
　
　そこで、数値微分よりも効率的に偏微分を処理するために、バックプロパゲーション（誤差逆伝播法）という手法を用います。

バックプロパゲーション（誤差逆伝播法）

　バックプロパゲーション は、ネットワークからの出力値と正解値（目標変数）の差分を上層へ伝えることによって順次重みを調整していく手法です。
　

　
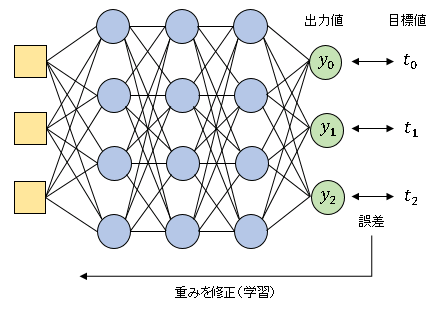
　深さ $d$ 層の分類用ニューラルネットワークのオンライン学習を考えます。すなわち、バッチサイズ は 1 であり、一度に 1 個のデータを与えて重みの更新を行ないます。
　
　損失関数は交差エントロピー誤差 $\displaystyle E=-\sum_{k}t_k\log y_k$ です。
　
　出力層の活性化関数は ソフトマックス関数 とします。
　
　話を具体的にするために、出力層（第 $d$ 層）は 3 個、その１つ上の層（第 $d-1$ 層）と２つ上の中間層（第 $d-2$ 層）は、それぞれ 2 個のニューロンで構成されるとします（下図参照）。
　

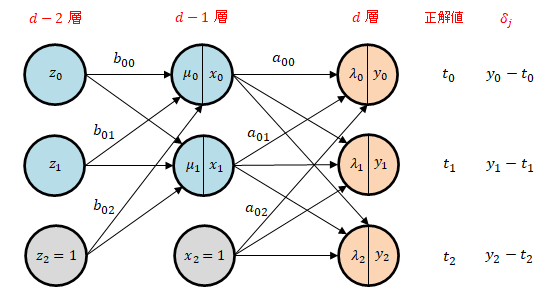
出力層における損失関数の勾配

　第 $d-1$ 層からの出力を $\boldsymbol{x}$、重み行列を $A$ とすると、第 $d$ 層の入力総和 $\boldsymbol{\lambda}$ は
　
\[\boldsymbol{\lambda}=A \boldsymbol{x}\tag{1}\]
で表されます。成分表示すると次のようになります。
　
\[\begin{bmatrix}\lambda_0\\ \lambda_1\\ \lambda_2\end{bmatrix}=\begin{bmatrix}a_{00} & a_{01} & a_{02}\\a_{10} & a_{11} &a_{12}\\a_{20} & a_{21} & a_{22}\end{bmatrix}
\begin{bmatrix}x_0\\x_1\\x_2\end{bmatrix}\tag{2}\]
　出力層における損失関数の勾配を求めてみましょう。
　偏微分の連鎖律によって、$\cfrac{\partial E}{\partial a_{ji}}$ は出力層の入力総和 $\lambda_j$ を使って
　
\[\frac{\partial E}{\partial a_{ji}}=\frac{\partial E}{\partial\lambda_{j}}\frac{\partial \lambda_j}{\partial a_{ji}}\tag{3}\]
と表すことができます。まず最初に、$\cfrac{\partial E}{\partial \lambda_{j}}$ を求めてみましょう。正解値（目標変数）を
　
\[\boldsymbol{t}=\begin{bmatrix}t_0\\t_1\\t_2\end{bmatrix}\]
とすると、交差エントロピー誤差は
　
\[E=-t_0\log y_0-t_1\log y_1-t_2\log y_2\tag{4}\]
なので、$E$ を $\lambda_0$ で微分すると
　
\[\frac{\partial E}{\partial \lambda_0}=-\frac{t_0}{y_0}\frac{\partial y_0}{\partial \lambda_0}-\frac{t_1}{y_1}\frac{\partial y_1}{\partial \lambda_0}-\frac{t_2}{y_2}\frac{\partial y_2}{\partial \lambda_0}\tag{5}\]
　出力層の活性化関数はソフトマックス関数
　
\[y_i=\frac{\exp(x_i)}{\displaystyle\sum_{i=1}^{n}\exp(x_i)}\tag{6}\]
に設定しています。ソフトマックス関数の微分は
　
\[\frac{\partial y_i}{\partial x_j}=\begin{cases}-y_iy_j & (i\neq j)\\[6pt]y_i(1-y_i) & (i=j)\end{cases}\tag{7}\]
で与えられます。式 (5) の続きを計算すると、
　
\[\begin{align*}\frac{\partial E}{\partial \lambda_0}&=-\frac{t_0y_0(1-y_0)}{y_0}-\frac{t_1(-y_1y_0)}{y_1}-\frac{t_2(-y_2y_0)}{y_2}\\[6pt]&=(t_0+t_1+t_2)y_0-t_0\end{align*}\tag{8}\]
　正解値の合計は $t_0+t_1+t_2=1$ となるので、
　
\[\frac{\partial E}{\partial \lambda_0}=y_0-t_0\tag{9}\]
が得られます。同様に
　
\[\frac{\partial E}{\partial \lambda_1}=y_1-t_1,\quad \frac{\partial E}{\partial\lambda_2}=y_2-t_2\tag{10}\]
となるので、
　
\[\frac{\partial E}{\partial \lambda_j}=y_j-t_j\tag{11}\]
となります。すなわち、交差エントロピー誤差の入力総和による微分は出力値 $y_j$ と目標変数 $t_j$ の差分となっています。この差分を $\delta_j$ と表すことにすると、出力層における勾配は
　
\[\frac{\partial E}{\partial \lambda_j}\delta_j\tag{12}\]
となります。
　
　次は $\cfrac{\partial \lambda_j}{\partial a_{ji}}$ の部分を求めてみます。たとえば $j=0$ のとき、
　
\[\lambda_0=a_{00}x_0+a_{01}x_1+a_{02}x_2\tag{13}\]
なので、
　
\[\frac{\partial \lambda_0}{\partial a_{00}}=x_0,\quad \frac{\partial \lambda_0}{\partial a_{01}}=x_1,\quad \frac{\partial \lambda_0}{\partial a_{02}}=x_2\tag{14}\]
となります。$j=1,\ 2$ のときも同様なので、
　
\[\frac{\partial \lambda_j}{\partial a_{ji}}=x_i\tag{15}\]
が得られます。式 (3) に (12) と (15) を代入すると、
　
\[\frac{\partial E}{\partial a_{ji}}=\delta_j x_i\tag{16}\]
となります。交差エントロピー誤差の勾配が
　
　　[出力値と正解値の差] × [１つ上の層からの入力値]
　
となっています。この計算はコンピュータにとっては単純な処理ですから、数千個の重みについて実行したとしても一瞬で終えることができます。

中間層における損失関数の勾配

　次は第 $d-1$ 層の勾配 $\cfrac{\partial E}{\partial b_{ji}}$ を求めます。
　第 $d-2$ 層からの出力を $\boldsymbol{z}$、重み行列を $B$ とすると、第 $d-1$ 層の入力総和 $\boldsymbol{\mu}$ は
　
\[\boldsymbol{\mu}=B\boldsymbol{z}\tag{17}\]
と表されます。成分表記すると以下のようになります。
　
\[\begin{bmatrix}\mu_0 \\ \mu_1\end{bmatrix}=\begin{bmatrix} b_{00} & b_{01} &b_{02}\\b_{10} & b_{11} & b_{12}\end{bmatrix}\begin{bmatrix}z_0 \\ z_1 \\z_2\end{bmatrix}\tag{18}\]
　偏微分の連鎖律によって、
　
\[\frac{\partial E}{\partial b_{ji}}=\frac{\partial E}{\partial \mu_{j}}\frac{\partial \mu_j}{\partial b_{ji}}\tag{19}\]
と表すことができます。(18) を $b_{ji}$ で微分すると、
　
\[\frac{\partial \mu_{j}}{\partial b_{ji}}=z_i\tag{20}\]
となるので、(19) は
　
\[\frac{\partial E}{\partial b_{ji}}=\frac{\partial E}{\partial \mu_{j}}z_{i}\tag{21}\]
と表せます。
　
　次に (19) の $\cfrac{\partial E}{\partial \mu_{j}}$ に連鎖律を適用すると
　
\[\frac{\partial E}{\partial \mu_{j}}=\frac{\partial E}{\partial x_j}\frac{\partial x_j}{\partial \mu_{j}}\tag{22}\]
と表せます。$\cfrac{\partial x_j}{\partial \mu_j}$ の部分は、$x_j$ が活性化関数 $f(u)$ によって調整された値であることから、
　
\[\frac{\partial x_j}{\partial \mu_j}=\frac{\partial f(\mu_j)}{\partial \mu_j}=f'(\mu_j)\tag{23}\]
と表しておくことにすると（具体的な表式は設定した活性化関数によって異なります）、(22) は
　
\[\frac{\partial E}{\partial \mu_{j}}=f'(\mu_j)\frac{\partial E}{\partial x_j}\tag{24}\]
となります。
　
　$\cfrac{\partial E}{\partial x_j}$ の計算はやや複雑です。$E$ は $\lambda_0(x_0,\ x_1,\ x_2)$, $\lambda_1(x_0,\ x_1,\ x_2)$, $\lambda_2(x_0,\ x_1,\ x_2)$ の関数なので、$E$ を $x_j$ で偏微分すると、これも連鎖律によって、
　
\[\frac{\partial E}{\partial x_j}=\frac{\partial E}{\partial \lambda_0}\frac{\partial \lambda_0}{\partial x_j}+\frac{\partial E}{\partial \lambda_1}\frac{\partial \lambda_1}{\partial x_j}+\frac{\partial E}{\partial \lambda_2}\frac{\partial \lambda_2}{\partial x_j}\tag{25}\]
と表せます。$\cfrac{\partial E}{\partial \lambda_j}$ は先に求めた出力値と正解値の差分 $\delta_j$ なので（この項を通して $\delta_j$ の情報が中間層まで伝えられていることに着目してください）、(25) は
　
\[\frac{\partial E}{\partial x_j}= \delta_{0}\frac{\partial \lambda_0}{\partial x_j}+\delta_{1}\frac{\partial \lambda_1}{\partial x_j}+\delta_{2}\frac{\partial \lambda_2}{\partial x_j}\tag{26}\]
となります。
　
　$\cfrac{\partial \lambda_r}{\partial x_j}\ (r=0,1,2)$ の部分は行列形式
　
\[\begin{bmatrix}\lambda_0\\ \lambda_1\\ \lambda_2\end{bmatrix}=\begin{bmatrix}a_{00} & a_{01} & a_{02}\\a_{10} & a_{11} & a_{12}\\a_{20} & a_{21} & a_{22}\end{bmatrix}
\begin{bmatrix}x_0\\x_1\\x_2\end{bmatrix}\tag{27}\]
の形のまま微分すると簡単です。たとえば $x_0$ で微分すると、
　
\[\frac{\partial}{\partial x_0}\begin{bmatrix}\lambda_0\\ \lambda_1\\ \lambda_2\end{bmatrix}=\begin{bmatrix}a_{00} & a_{01} & a_{02}\\a_{10} & a_{11} & a_{12}\\a_{20} & a_{21} & a_{22}\end{bmatrix}\begin{bmatrix}1\\0\\0\end{bmatrix}=\begin{bmatrix}a_{00}\\a_{10}\\a_{20}\end{bmatrix}\tag{28}\]
となって、$A$ の $0$ 列目が抜き出されます。同様に $x_1,\ x_2$ で微分すると $1$ 列目、$2$ 列目が抜き出されるので、
　
\[\frac{\partial}{\partial x_j}\begin{bmatrix}\lambda_0\\ \lambda_1\\ \lambda_2\end{bmatrix}=\begin{bmatrix}a_{0j}\\a_{1j}\\a_{2j}\end{bmatrix}\tag{29}\]
と表せます。したがって、(26) は
　
\[\frac{\partial E}{\partial x_j}=a_{0j}\delta_0+a_{1j}\delta_1+a_{2j}\delta_2\tag{30}\]
となります。(24) に代入すると、
　
\[\frac{\partial E}{\partial \mu_{j}}=f'(\mu_j)(a_{0j}\delta_0+a_{1j}\delta_1+a_{2j}\delta_2)\tag{31}\]
　この式を一般化すると、
　
\[\frac{\partial E}{\partial \mu_j}=f'(\mu_j)\sum_{r}a_{rj}\delta_r\tag{32}\]
となります。$\displaystyle\sum_{r}$ は出力層のニューロンの個数だけ和をとることを意味します（たとえば、$10$ 個のニューロンがある場合は $r=0$ から $r=9$ まで和をとります）。
　
　式 (21) より、この層の重みによる損失関数の勾配は
　
\[\frac{\partial E}{\partial b_{ji}}=z_if'(\mu_j)\sum_{r}a_{rj}\delta_r\tag{33}\]
となります。

重みの更新式

　最後に層同士の関係を明確にするために、以下のように変数を置き換えます。
　
\[\begin{align*}&x_j=y_j^{(d-1)},\quad z_j=y_j^{(d-2)}\tag{34}\\[6pt]&\lambda_j=u_j^{(d)},\quad \mu_j=u_j^{(d-1)}\tag{35}\\[6pt]&a_{ji}=w_{ji}^{(d)},\quad b_{ji}=w_{ji}^{(d-1)}\tag{36}\end{align*}\]
　右上の添字は層番号を意味します (たとえば、$u_j^{(d)}$ は $d$ 層、すなわち出力層のニューロンの入力総和であることを表しています)。　ただし、最終的な出力値 $y_j$、および正解値と出力値の差分 $\delta_j=t_j-y_j$については、層番号を表示しないことにします（下図参照）。
　

　
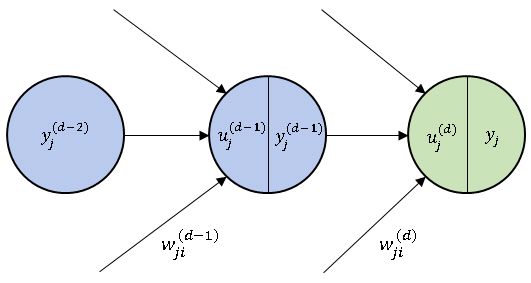
　新しい変数で $\cfrac{\partial E}{\partial a_{ji}}$ を書き直すと次のようになります。
　
\[\frac{\partial E}{\partial w_{ji}^{(d)}}=y_i^{(d-1)}\delta_j\tag{37}\]
　同様に、$\cfrac{\partial E}{\partial b_{ji}}$ を書き直すと、
　
\[\frac{\partial E}{\partial w_{ji}^{(d-1)}}=y_i^{(d-2)}f'(u_j^{(d-1)})\sum_{r}w_{rj}^{(d)}\delta_r\tag{38}\]
となります。ここで、
　
\[f'(u_j^{(d-1)})\sum_{r}w_{rj}^{(d)}\delta_r=\delta_j^{(d-1)}\tag{39}\]
と定義すると、
　
\[\frac{\partial E}{\partial w_{ji}^{(d-1)}}=y_i^{(d-2)}\delta_j^{(d-1)}\tag{40}\]
となります。(37) と (40) より、出力層および、その１つ手前の中間層の重みの更新は
　
\[\begin{align*}&w_{ji}^{(d)}(t+1)=w_{ji}^{(d)}(t)-\alpha\frac{\partial E}{\partial w_{ji}^{(d)}}=w_{ji}^{(d)}(t)-\alpha\delta_jy_i^{(d-1)}\\[6pt]&w_{ji}^{(d-1)}(t+1)=w_{ji}^{(d-1)}(t)-\alpha\frac{\partial E}{\partial w_{ji}^{(d-1)}}=w_{ji}^{(d-1)}(t)-\alpha\delta_j^{(d-1)}y_i^{(d-2)}\end{align*}\tag{41}\]
で与えられます ($\alpha$ は学習率で正の値をとります)。同様に、さらに上の層も
　
\[w_{ji}^{(d-2)}(t+1)=w_{ji}^{(d-2)}(t)-\alpha\delta_j^{(d-2)}y_i^{(d-3)}\tag{42}\]
というように遡って計算してくことができます。これでバックプロパゲーションを Python に実装することができますが、次回記事では、更新式の意味するところをもう少し掘り下げて解説したいと思います。

【おすすめ書籍】ゼロから作る Deep Learning

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装 中古価格 ￥2,818から (2019/7/30 20:24時点)

ゼロから作るDeep Learning ? ?自然言語処理編 中古価格 ￥2,979から (2020/8/20 11:36時点)

ゼロから作るDeep Learning ? ?フレームワーク編 中古価格 ￥3,500から (2020/8/20 11:38時点)