【Pythonで学ぶ線形代数学講座(6)】ベクトルの線形独立と線形従属
ベクトルの線形結合
ベクトル $\boldsymbol{v},\ \boldsymbol{w}$ について、それぞれに任意の実数 $p,\ q$ を掛けて加えたベクトル $\boldsymbol{r}$ を $\boldsymbol{v}$ と $\boldsymbol{w}$ の 線形結合（linear combination）とよびます。
\[\boldsymbol{r}=p\boldsymbol{v}+q\boldsymbol{w}\tag{1}\]
$\boldsymbol{v}$ と $\boldsymbol{w}$ が互いに平行でない 2 次元ベクトルであれば、$p$ と $q$ はすべての実数を動くので、$\boldsymbol{r}$ は平面上のすべての点を表します。このとき $p$ と $q$ は、下図にあるような斜交座標系上の点とみなすことができます。
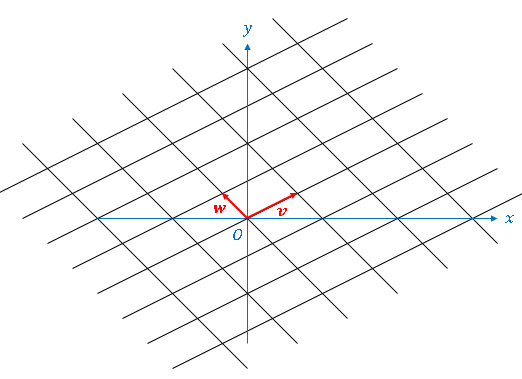
ベクトル $\boldsymbol{v}$ と $\boldsymbol{w}$ は、この座標系の 基底 とよばれます。
この定義にしたがうと、普段よく使っているデカルト座標系（直交座標系）は、
$\begin{bmatrix}1\\0\end{bmatrix}$ と $\begin{bmatrix}0\\1\end{bmatrix}$ を基底とする座標系です。
ベクトル $\boldsymbol{v}$ と $ \boldsymbol{w}$ が平行であるとき、すなわち $\boldsymbol{w}=k\boldsymbol{v}$ と表せるとき、線形結合は
\[\boldsymbol{r}=p\boldsymbol{v}+q\boldsymbol{w}=p\boldsymbol{v}+qk\boldsymbol{v}=(p+qk)\boldsymbol{v}\]
となります。これはベクトルのスカラー倍であり、1 本の直線を表す式なので平面を作ることはできません。
線形独立と線形従属
$n$ 個のベクトルの集合 $\{\boldsymbol{v}_1,\ \boldsymbol{v}_2,\ \cdots,\ \boldsymbol{v}_n\}$ が与えられたとします。
この集合から任意のベクトル $\boldsymbol{v}_k$ を選んだとき、残りすべてのベクトルの線形結合で表すことができなければ $\{\boldsymbol{v}_1,\ \boldsymbol{v}_2,\ \cdots,\ \boldsymbol{v}_n\}$ は互いに 線形独立 であるといいます。
逆に集合に含まれるいずれか１つのベクトルが残りのベクトルの線形結合として表すことができるのならば、$\{\boldsymbol{v}_1,\ \boldsymbol{v}_2,\ \cdots,\ \boldsymbol{v}_n\}$ は互いに 線形従属 であるといいます。
最も簡単な例として、2 つのベクトルだけで構成される集合
\[U=\left\{\begin{bmatrix}1\\0\end{bmatrix}, \quad \begin{bmatrix}0\\1\end{bmatrix}\right\}\]
を考えます。$\begin{bmatrix}1\\0\end{bmatrix}$ を定数倍して $\begin{bmatrix}0\\1\end{bmatrix}$ をつくることはできないし、$\begin{bmatrix}0\\1\end{bmatrix}$ を定数倍して $\begin{bmatrix}1\\0\end{bmatrix}$ をつくることもできません。
したがって、$\begin{bmatrix}1\\0\end{bmatrix}$ と $\begin{bmatrix}0\\1\end{bmatrix}$ は互いに線形独立です。
次は上の集合 $U$ に $\begin{bmatrix}3\\3\end{bmatrix}$ を加えてみます。
\[V=\left\{\begin{bmatrix}1\\0\end{bmatrix},\quad \begin{bmatrix}0\\1\end{bmatrix},\quad \begin{bmatrix}3\\3\end{bmatrix}\right\}\]
$\begin{bmatrix}3\\3\end{bmatrix}$ と $\begin{bmatrix}1\\0\end{bmatrix}$ は平行ではないし、$\begin{bmatrix}3\\3\end{bmatrix}$ と $\begin{bmatrix}0\\1\end{bmatrix}$ も平行ではありませんが、
\[\begin{bmatrix}3\\3\end{bmatrix}=3\begin{bmatrix}1\\0\end{bmatrix}+3\begin{bmatrix}0\\1\end{bmatrix}\]
のように他の 2 本のベクトルの線形結合で表されるので、集合 $V$ の各ベクトルは互いに線形従属の関係にあります。2 次元空間 (平面) では 2 本の互いに独立なベクトルで全平面を張れるので、3 本以上のベクトルで構成される集合は必ず線形従属となります。
2 つの 2 次元ベクトルの間で成り立つ線形独立と線形従属を表す公式を導いておきます。
$\boldsymbol{v}=\begin{bmatrix}v_1\\v_2\end{bmatrix}$ と $ \boldsymbol{w}=\begin{bmatrix}w_1\\w_2\end{bmatrix}$ が 線形従属であるときは、
\[\begin{bmatrix}w_1\\w_2\end{bmatrix}=k\begin{bmatrix}v_1\\v_2\end{bmatrix}\]
と表せるので、
\[v_1w_2-v_2w_1=kv_1v_2-kv_2v_1=0\]
が成り立ちます。ベクトルが線形独立であるときには、
\[v_1w_2-v_2w_1\neq 0\]
となります。証明は省略しますが、この逆も成り立ちます。すなわち、$v_1w_2-v_2w_1=0$ であれば $\boldsymbol{v}$ と $\boldsymbol{w}$ は線形従属であり、$v_1w_2-v_2w_1\neq 0$ であれば $\boldsymbol{v}$ と $\boldsymbol{w}$ は線形独立です。
コメント
【AI連載小説】科学とコードの交差点(65)
「ベクトルの線形結合を実装しよう」
開誠（サークルの部屋でコンピュータを前にして）：「みんな、今日は線形結合についてやるよ」
明信：「いいね。線形結合って、何か面白そうなことができるのか？」
開誠：「そうだよ。線形結合はベクトルの新たなベクトルを作り出す方法の一つだ。例えば、ベクトル v1 と v2 があるとき、c1・v1 + c2・v2 のように、係数 c1 と c2 を調整することで新しいベクトルを作ることができる」
美純：「それは面白そう。どんなことができるの？」
開誠：「例えば、ベクトルを組み合わせて新しいベクトルで方向を変えたり、特定の条件を満たすベクトルを作り出すことができるんだ」
明信：「具体的な例を見せてくれる？」
開誠：「もちろん。例えば、2つのベクトル v1 =[1,2] と v2 =[3,1] があるとしよう。これを線形結合で新しいベクトルを作り出すコードを書いてみよう。」
開誠がPythonコードを書きながら説明します。
import numpy as np def linear_combination(v1, v2, c1, c2): """ 2つのベクトル v1, v2 と係数 c1, c2 を受け取り、線形結合を計算する関数。 """ result_vector = c1 * v1 + c2 * v2 return result_vector # 例として、ベクトル v1, v2 を定義 v1 = np.array([1, 2]) v2 = np.array([3, 1]) # 係数を設定 c1 = 2 c2 = -1 # 線形結合を計算 result = linear_combination(v1, v2, c1, c2) print(f"線形結合 {c1}*v1 + {c2}*v2 の結果: {result}")美純：「なるほど、これで新しいベクトルが得られるんだね」
開誠：「そうだ。線形代数の応用でよく使われるテクニックだから、覚えておくと役立つよ」