固有値と固有ベクトル

行列の固有値と固有ベクトル

　行列 $A=\begin{bmatrix}2&1\\1&2\end{bmatrix}$ によってベクトル $\boldsymbol{x}=\begin{bmatrix}x\\y\end{bmatrix}$ を 線型変換 してみます。
　
\[\begin{bmatrix}2&1\\1&2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=x\begin{bmatrix}2\\1\end{bmatrix}+y\begin{bmatrix}1\\2\end{bmatrix}\]
　右辺のベクトルは基底 $\begin{bmatrix}2\\1\end{bmatrix}$ と $\begin{bmatrix}1\\2\end{bmatrix}$ の線型結合を表しています。
　
　たとえば、ベクトル $\begin{bmatrix}1\\1\end{bmatrix}$ を $A$ で変換することは、2 つの基底を同じ重みで加えることを意味します（下図）。　
　
\[\begin{bmatrix}2&1\\1&2\end{bmatrix}\begin{bmatrix}1\\1\end{bmatrix}=\begin{bmatrix}2\\1\end{bmatrix}+\begin{bmatrix}1\\2\end{bmatrix}=3\begin{bmatrix}1\\1\end{bmatrix}\]

　
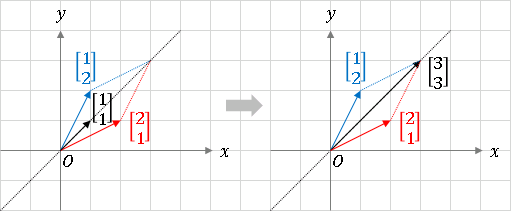
　ベクトル $\begin{bmatrix}1\\1\end{bmatrix}$ は自身を $3$ 倍に伸ばしたベクトルに変換されています。
　$x$ と $y$ が等しい点、すなわち直線 $y=x$ 上の点を $A$ で変換すると、2 つの基底に同じ係数を掛けて加えることになるので、
　
\[\begin{bmatrix}2\\2\end{bmatrix},\quad \begin{bmatrix}3\\3\end{bmatrix},\quad \begin{bmatrix}4\\4\end{bmatrix}\, \cdots\]
などもすべて $A$ によって自身を定数倍するようなベクトルですが、これらは $\begin{bmatrix}1\\1\end{bmatrix}$ に平行なベクトルなので本質的に同じものです。
　
　しかし、下図にあるように基底 $\begin{bmatrix}1\\2\end{bmatrix}$ に $-1$ を掛けて、もう１つの基底 $\begin{bmatrix}2\\1\end{bmatrix}$ に加えると、
　
\[\begin{bmatrix}2\\1\end{bmatrix}-\begin{bmatrix}1\\2\end{bmatrix}=\begin{bmatrix}1\\-1\end{bmatrix}\]
となるので、$\begin{bmatrix}1\\-1\end{bmatrix}$ もまた $A$ によって自身を変えない (回りくどい言い方をすれば自身を $1$ 倍する) ベクトルです。
　

　
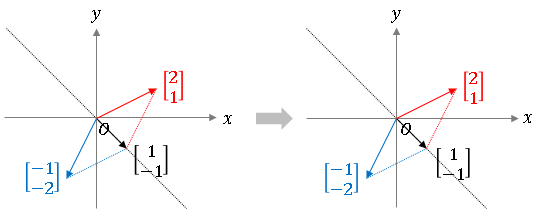
　このベクトルは $\begin{bmatrix}1\\1\end{bmatrix}$ に平行ではありません (線型独立です)。

固有値と固有ベクトルの求め方

　一般に行列 $A$ と $\boldsymbol{0}$ でないベクトル $\boldsymbol{x}$ について、
　
\[A\boldsymbol{x}=\lambda\boldsymbol{x}\tag{1}\]
を満たすようなスカラー $\lambda$ を $A$ の 固有値 (eigenvalue)、ベクトル $\boldsymbol{x}$ を $A$ の 固有ベクトル (eigenvector) と定義します。ちなみにギリシャ文字 $\lambda$ は「ラムダ」とよびます。
　
　(1) は 単位行列 $I$ を用いて
　
\[A\boldsymbol{x}=\lambda I\boldsymbol{x}\tag{2}\]
と書くこともできます。$\lambda I \boldsymbol{x}$ を左辺に移項すると、
　
\[(A-\lambda I)\boldsymbol{x}=\boldsymbol{0}\tag{3}\]
となります。ここで
　
\[A-\lambda I=\begin{bmatrix}a&b\\c&d\end{bmatrix}\tag{4}\]
とおくと、方程式 (3) は
　
\[x\begin{bmatrix}a\\c\end{bmatrix}+y\begin{bmatrix}b\\d\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}\tag{5}\]
と表せます。
　
　このとき、$\begin{bmatrix}a\\c\end{bmatrix}$ と $\begin{bmatrix}b\\d\end{bmatrix}$ が線型独立の関係にあると、$x=y=0$ とする以外に 2 本のベクトルをつないで $\begin{bmatrix}0\\0\end{bmatrix}$ をつくることはできません。$\boldsymbol{x}$ は $\boldsymbol{0}$ でないという条件がついているので、$\begin{bmatrix}a\\c\end{bmatrix}$ と $\begin{bmatrix}b\\d\end{bmatrix}$ は線型従属である必要があります。『行列式』の記事で学んだように、この 2 本のベクトルが線型従属であることと、$A-\lambda I$ の行列式が $0$ であることは等価です。すなわち (3) は
　
\[\det (A-\lambda I)=0\tag{6}\]
という方程式に置き換えられます。(6) を $A$ の 固有方程式 (characteristic equation) とよびます。
　
　例として行列

\[A=\begin{bmatrix}3&1\\2&4\end{bmatrix}\]
の固有値と固有ベクトルを求めてみましょう。$\det(A-\lambda I)$ を計算すると
　
\[\begin{align*}\det(A-\lambda I)&=(3-\lambda)(4-\lambda)-2\\[6pt]&=\lambda^2-7\lambda+10\\[6pt]&=(\lambda-2)(\lambda-5)\end{align*}\]
なので、$\det(A-\lambda I)=0$ とおくと固有値 $\lambda=2,\ 5$ が得られます。$\lambda=2$ のときは
　
\[\begin{bmatrix}3&1\\2&4\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=2\begin{bmatrix}x\\y\end{bmatrix}\tag{7}\]
という線型変換を満たすように $x$ と $y$ を決めます。
　
\[\begin{align*}3x+2y&=2x\\[6pt]2x+4y&=2y\end{align*}\]
を解くと $y=-x$ が得られます。これは $y=-x$ の関係を満たすベクトルはすべて $A$ による変換で 2 倍に引き伸ばされることを意味します。たとえば $x=1$ を選べば、$y=-1$ なので、
　
\[\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}1\\-1\end{bmatrix}\tag{8}\]
が求める固有ベクトルのひとつです。同じようにして
　
\[\begin{bmatrix}3&1\\2&4\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=5\begin{bmatrix}x\\y\end{bmatrix}\tag{9}\]
を解くと $y=2x$ が得られるので、(8) と線型独立な固有ベクトルとして
　
\[\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}1\\2\end{bmatrix}\tag{10}\]
を選ぶことができます。
　

numpy.linalg.eig()

　numpy.linalg.eig() は行列の固有値と固有ベクトルをタプルで返します。

# numpy_eigenvalue_eigenvector

# In[1]

import numpy as np

# 2×2正方行列を定義
a = np.array([[3, 1],
              [2, 4]])

# aの固有値と固有ベクトル
# インデクス0に固有値、インデクス1に固有ベクトルが格納される
a_eig = np.linalg.eig(a)

# 固有値を表示
print("固有値 {}\n".format(a_eig[0]))

# 固有ベクトルを表示
print("固有ベクトル\n{}".format(a_eig[1]))

固有値 [2. 5.]

固有ベクトル
[[-0.70710678 -0.4472136 ]
 [ 0.70710678 -0.89442719]]

　固有値 2 に対応する固有ベクトルは縦ベクトル

　[[-0.70710678],
　 [0.70710678]]

であることに注意してください。

numpy.linalg.eigvals()

　numpy.linalg.eigvals() は行列の固有値を返します。

# numpy_eigenvalue

# In[1]

import numpy as np

# 2×2正方行列を定義
b = np.array([[7, 11],
              [5,  9]])

# bの固有値
b_eig = np.linalg.eigvals(b)

print(b_eig)

[ 0.51668523 15.48331477]

scipy.linalg.eig()

　scipy.linalg.eig() は行列の固有値と固有ベクトルを返します。
　戻り値のデータ型は常に complex (複素数型) です。

# scipy_eigenvalue_eigenvector

# In[1]

import numpy as np
from scipy import linalg

# 2×2正方行列を定義
a = np.array([[-5 + 2j, 7 + 1j],
              [      3, 1 + 3j]])

# aの固有値と固有ベクトル
a_eig = linalg.eig(a)

# 固有値を表示
print("固有値 {}\n".format(a_eig[0]))

# 固有ベクトルを表示
print("固有ベクトル\n{}".format(a_eig[1]))

固有値 [-7.48174295+1.95272881j  3.48174295+3.04727119j]

固有ベクトル
[[ 0.94355342+0.j          0.6373659 +0.01214028j]
 [-0.32872404+0.04058874j  0.77046565+0.j        ]]

scipy.linalg.eigvals()

　scipy.linalg.eigvals() は行列の固有値を返します。
　戻り値のデータ型は常に complex (複素数型) となります。

# scipy_eigenvalue

# In[1]

import numpy as np
from scipy import linalg

# 3×3正方行列を定義
b = np.array([[0, 4, 1],
              [7, 3, 5],
              [2, 7, 8]])

# bの固有値
b_eig = linalg.eigvals(b)

print(b_eig)

[13.28705108+0.j -4.59598642+0.j  2.30893534+0.j]