【Pythonで学ぶ線形代数学講座(14)】線形写像
集合と写像
ある 2 つの集合 $A,\ B$ があって、$A$ のそれぞれの元 (要素) について、$B$ の元 (要素) に対応させるような規則 $f$ が与えられたとき、$f$ を $A$ から $B$ への写像(map)とよび、
\[f:A \mapsto B\]
のように記述します。たとえば、元を図 1 のように結びつけて、これを写像 $f$ と定義することができます。
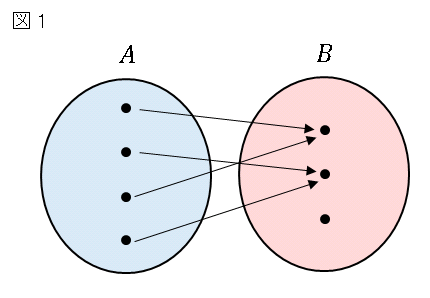
結びつけ方は自由です。とにかく「このように対応させる」と決めたなら、それが写像 $f$ となります。また、図 1 のように、$B$ のある元に対して、$A$ の複数の元が対応しても構いません。
定義域と値域(像)
写像 $f:A \mapsto B$ において、集合 $A$ を写像 $f$ の定義域といいます。また、集合 $A$ の写像 $f$ による移り先全体を写像 $f$ の値域、あるいは像(image)とよび、$f(A)$ または $\mathrm{Im}f$ で表します。
$B$ と $f(A)$ は異なる集合です。$f(A)$ は図 2 のオレンジ色に塗られた部分です。$f(A)$ は $B$ に含まれますが必ずしも一致しているとは限りません。

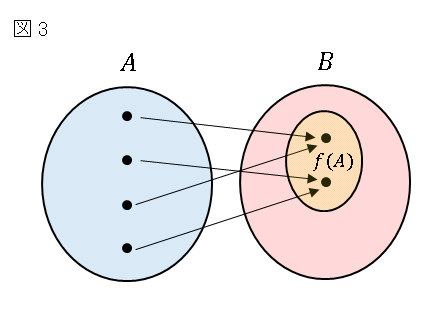
しかし、図 3 のように、集合 $B$ と $f(A)$ が完全に一致しているとき、$f$ は $A$ から $B$ への全射(surjection)であるといいます。
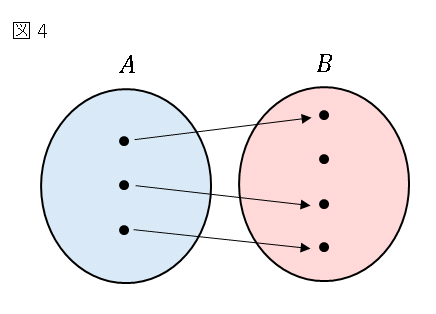
また、図 4 にあるように、$A$ の異なる元に対して $B$ の異なる元が対応するとき、$f$ は $A$ から $B$ への 単射 (injection) であるといいます。
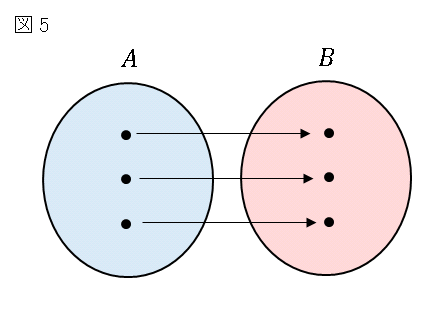
そして図 5 のように、全射かつ単射であるとき、$f$ は $A$ から $B$ への 全単射 (bijection) であるといいます。
写像 $f:A \mapsto B$ が全単射であれば、$B$ から $A$ への逆写像 $f^{-1}:B \mapsto A$ を定義することができます。
線形写像
線形写像
$x$ の 写像 $f(x)$ が 線形 であるとは、$f$ が次の 2 つの性質を満たす操作であることを意味します。
\[\begin{align*}&f(x+y)=f(x)+f(y)\tag{1}\\[6pt]&f(kx)=kf(x)\tag{2}\end{align*}\]
これは次のように 1 つの式にまとめて表すこともできます。
\[f(\alpha x+\beta y)=f(\alpha x)+f(\beta y)\tag{3}\]
たとえば、原点を通る一次関数 $f(x)=ax$ は、
\[\begin{align*}&a(x+y)=ax+ay\\[6pt]&a(kx)=k(ax)\end{align*}\]
となるので線形写像です。二次関数 $f(x)=ax^2$ は
\[a(x+y)^2=a(x^2+2xy+y^2)\neq ax^2+ay^2\]
なので線形写像ではありません。
任意の関数 $x(t)$ の $t$ による微分操作は
\[\begin{align*}&\frac{d}{dt}(x(t)+y(t))=\frac{dx(t)}{dt}+\frac{dy(t)}{dt}\\[6pt]&\frac{d}{dt}(ax(t))=a\frac{dx(t)}{dt}\end{align*}\]
となるので線形写像です。このように数学では色々な場面で線形写像が登場しますが、線形代数では数のグループ、すなわちベクトル $\boldsymbol{u}$ についての線形写像を扱います:
\[\begin{align*}&f(\boldsymbol{u}+\boldsymbol{v})=f(\boldsymbol{u})+f(\boldsymbol{v})\tag{4}\\[6pt]&f(k\boldsymbol{u})=kf(\boldsymbol{v})\tag{5}\end{align*}\]
あるいは 1 つの式にまとめて
\[f(\alpha\boldsymbol{u}+\beta\boldsymbol{v})=\alpha f(\boldsymbol{u})+\beta f(\boldsymbol{v})\tag{6}\]
という性質を満たす写像です。
線形変換
一般にベクトル空間 $V$ からベクトル空間 $V’$ への線形写像は 線形変換 (一次変換)とよばれます。そして、すべての線形変換は行列を使って
\[A\boldsymbol{u}=\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}\tag{7}\]
の形式で表現できることが知られています。このとき、$A$ のことを $f$ の 表現行列 とよびます。たとえば、任意のベクトルを 2 倍するという変換は
\[\begin{bmatrix}2&0\\0&2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}
=\begin{bmatrix}2x\\2y\end{bmatrix}\tag{8}\]
のように表すことができます。もう少し先の記事で具体的に扱いますが、行列を使って点(あるいは点の集合)を $x$ 軸または $y$ 軸について対称移動させたり、原点の回りに回転させたりすることもできます。
合成写像
$f(x)$ の $g$ による写像 $g(f(x))$ を $f$ と $g$ の合成写像とよび、$g\circ f$ で表します。
$f$ と $g$ が線形写像であるときは、$g\circ f$ も線形写像です。
ベクトル $\boldsymbol{u}$ に対する線形変換 $f(\boldsymbol{u})$ と $g(\boldsymbol{u})$ が
\[f(\boldsymbol{u})=A\boldsymbol{u},\quad g(\boldsymbol{u})=B\boldsymbol{u}\tag{9}\]
で表されるとき、合成変換 $g\circ f$ は行列積 $BA$ によって表されます。
\[g\circ f(\boldsymbol{u})=BA\boldsymbol{u}\tag{10}\]
一般に行列積については交換法則が成り立たないので、$g\circ f$ と $f\circ g$ は異なる結果になることがあります。
ちなみに「写像」という概念はプログラミングのマッピング(個々の要素に、別の集合の要素を割り当てる操作)に応用されています。一例として、Python には map() という関数が用意されていて、シーケンスの各要素に同一規則を適用して、別のシーケンスを生成することができます。

コメント