グラム・シュミットの直交化法

グラム・シュミットの直交化法

前回記事では完全正規直交系の定義と性質について解説しました。今回は $\mathbb{R}^n$ の任意の基底 $\{\boldsymbol{a}_1,\ \boldsymbol{a}_2,\ ...,\ \boldsymbol{a}_n\}$ から完全正規直交系 $\{\boldsymbol{q}_1,\ \boldsymbol{q}_2,\ ...,\ \boldsymbol{q}_n\}$ をつくる グラム・シュミットの直交化法 を学びます。

直交化の手順

$\mathbb{R}^3$ を張る任意の基底 $\{\boldsymbol{a}_1,\ \boldsymbol{a}_2,\ \boldsymbol{a}_3\}$ が与えられたとします。
この基底を使って完全正規直交系 $\{\boldsymbol{q}_1,\ \boldsymbol{q}_2,\ \boldsymbol{q}_3\}$ をつくってみます。
最初に基底から適当なベクトルを 1 つ選んで $\boldsymbol{u}_1$ とします。
選び方は自由ですが、とりあえず $\boldsymbol{a}_1$ を選んで $\boldsymbol{u}_1=\boldsymbol{a}_1$ としましょう。

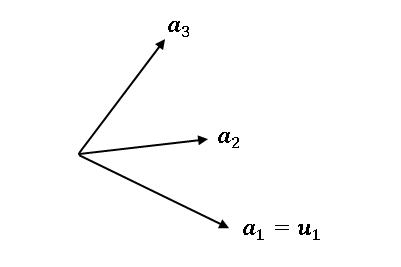
自身の大きさで割って ノルム を $1$ にしたベクトルを $\boldsymbol{q}_1$ とします。

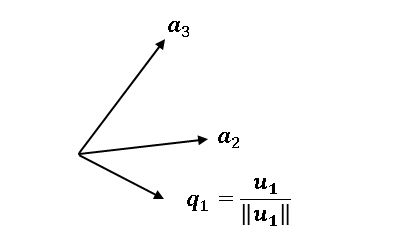
次に $\boldsymbol{a}_2$ を選んで、$\boldsymbol{q}_1$ への 射影ベクトル $\boldsymbol{p}_1$ を求めます。
 \[\boldsymbol{p}_1=\frac{\boldsymbol{q}_1^T\boldsymbol{a}_2}{\boldsymbol{q}_1^T\boldsymbol{q}_1}\boldsymbol{q}_1\tag{1}\]
$\boldsymbol{q}_1$ のノルムは $1$ なので、$\boldsymbol{q}_1^T\boldsymbol{q}_1=1$ となります。したがって、
 \[\boldsymbol{p}_1=(\boldsymbol{q}_1^T\boldsymbol{a}_2)\boldsymbol{q}_1\tag{2}\]
$\boldsymbol{a}_2$ から $\boldsymbol{p}_1$ を差し引くと、$\boldsymbol{q}_1$ に垂直なベクトルが得られます。これを $\boldsymbol{u}_2$ とします。
 \[\boldsymbol{u}_2=\boldsymbol{a}_2-\boldsymbol{p}_1
=\boldsymbol{a}_2-(\boldsymbol{q}_1^T\boldsymbol{a}_2)\boldsymbol{q}_1\tag{3}\]

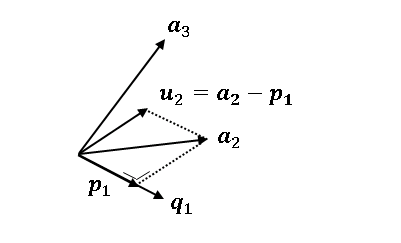
これも $\parallel\boldsymbol{u}_2\parallel$ で割って、ノルム $1$ のベクトル $\boldsymbol{q}_2$ をつくります。

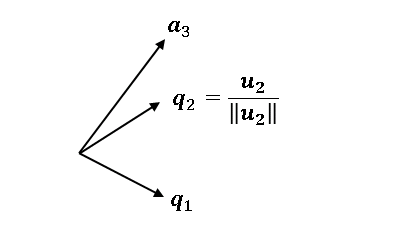
次は $\boldsymbol{q}_1$ と $\boldsymbol{q}_2$ の張る平面に対して $\boldsymbol{a}_3$ の射影ベクトル
 \[\boldsymbol{p}_2=(\boldsymbol{q}_1^T\boldsymbol{a}_3)\boldsymbol{q}_1+(\boldsymbol{q}_2^T\boldsymbol{a}_3)\boldsymbol{q}_2\tag{4}\]
をつくって $\boldsymbol{a}_3$ から差し引くと、$\boldsymbol{q}_1$ と $\boldsymbol{q}_2$ に垂直なベクトル $\boldsymbol{u}_3$ を得ます。
 \[\boldsymbol{u}_3=\boldsymbol{a}_3-(\boldsymbol{q}_1^T\boldsymbol{a}_3)\boldsymbol{q}_1-(\boldsymbol{q}_2^T\boldsymbol{a}_3)\boldsymbol{q}_2\tag{5}\]

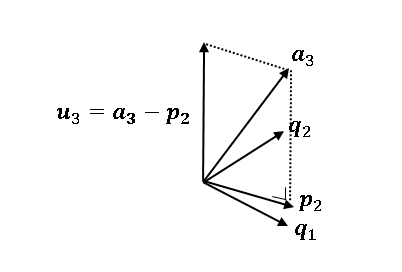
$\boldsymbol{u}_3$ を自身の大きさで割って $\boldsymbol{q}_3$ を得ます。

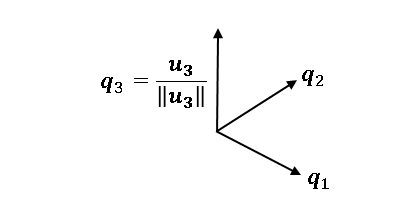
さらに次元の大きな空間の場合も同様にして、
 \[\boldsymbol{u}_k=\boldsymbol{a}_k-\sum_{i=1}^{k-1}(\boldsymbol{q}_i^T\boldsymbol{a}_k)\boldsymbol{q}_i,\quad\boldsymbol{q}_k=\frac{\boldsymbol{u}_k}{\parallel\boldsymbol{u}_k\parallel}\tag{6}\]
によって順次 $\boldsymbol{q}_k$ を求めていくことができます。新しい $\boldsymbol{q}_k$ を計算するときには、それまで求めた $\{\boldsymbol{q}_1,\ \boldsymbol{q}_2,\ ...\}$ をすべて使います。

Pythonで直交化法を実装する

グラム・シュミットの直交化法 を使って、基底を直交化するコードです。

# python_gram_schmidt_orthonormalization

# In[1]

import numpy as np
from scipy import linalg

# グラム・シュミット直交化関数
def schmidt(arr):

    # 配列のデータ型を64バイト浮動小数点数型に変換
    arr = np.array(arr, dtype=np.float64)

    # 渡した配列の列数(基底に含まれるベクトル数)
    k = arr.shape[1]

    # 1列目のベクトルを選択
    u = arr[:,[0]]

    # uを正規化
    q = u / linalg.norm(u)

    # シュミットの直交化
    for j in range(1, k):
        u = arr[:,[j]]
        for i in range(j):
            u -= np.dot(q[:,i], arr[:,j]) * q[:,[i]]
        qi = u / linalg.norm(u)
        q = np.append(q, qi, axis=1)
    return q

schmidt() に適当な基底を渡して完全正規直交系をつくってみます。

# In[2]

A = np.array([[3, 1, 1],
              [1, 0, 1],
              [2, 5, 0]])

Q = schmidt(A)

print(Q)
# [[ 0.80178373 -0.47847438 -0.35805744]
#  [ 0.26726124 -0.24880668  0.93094934]
#  [ 0.53452248  0.8421149   0.07161149]]

出力結果が完全正規直交系の性質を満たしているか確認しておきましょう。各々のベクトルは互いに直交します。たとえば、$1$ 列目のベクトルと $2$ 列目のベクトルの内積は $0$ となっているはずです。

# In[3]

print(Q[:, 0] @ Q[:, 1])
# -5.551115123125783e-17

前回学んだように、直交行列 $Q$ を適当なベクトルに作用させるとノルムが保存されます。

# In[4]

# ベクトルvを定義
v = np.array([[1],
              [2],
              [3]])

# Qvを計算
Qv = np.dot(Q, v)

# vとQvのノルム(大きさ)
v_norm = linalg.norm(v)
Qv_norm = linalg.norm(Qv)

print(v_norm)
print(Qv_norm)
# 3.7416573867739413
# 3.7416573867739418