正射影ベクトルと射影行列

≪【前の記事】直交補空間

正射影ベクトルと射影行列

今回の記事ではベクトルを互いに垂直な 2 つのベクトルに分解する手法を学びます。物理学を学んだことのある人にとっては、物体に作用する力の分解などでお馴染みの作業です。しかし、ベクトルの分解には、そうした便宜的手法以上の深い意味が隠されています。

直線への正射影

下図のように、2 つのベクトル $\boldsymbol{v},\ \boldsymbol{a}$ が与えられたとします。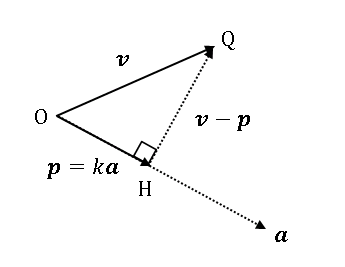$\boldsymbol{v}$ の終端 $\mathrm{Q}$ から $\boldsymbol{a}$ に沿う直線に垂線を下ろし、この直線と交わる点を $\mathrm{H}$ とします。このとき $\mathrm{O}$ を始点、$\mathrm{H}$ を終点とするベクトル $\boldsymbol{p}$ を $\boldsymbol{v}$ の $\boldsymbol{a}$ に対する 正射影ベクトル とよびます。
　
直感的には、$\boldsymbol{a}$ に垂直な光を $\boldsymbol{v}$ に当てたときに、直線 $OH$ に落ちる影が正射影です。 $\boldsymbol{p}$ は $\boldsymbol{a}$ に平行なので、$\boldsymbol{p}=k\boldsymbol{a}$ の形で表せるはずです。最初の図にあるように、$\boldsymbol{v}-\boldsymbol{p}$ は $\boldsymbol{a}$ に垂直なので、内積をとると $0$ になります。すなわち条件式
 \[\boldsymbol{a}^T(\boldsymbol{v}-k\boldsymbol{a})=0\tag{1}\]
を使って $k$ を求めると
 \[k=\frac{\boldsymbol{a}^T\boldsymbol{v}}{\boldsymbol{a}^T\boldsymbol{a}}\tag{2}\]
となります。分母は同じベクトルの内積なので、$\parallel\boldsymbol{a}\parallel^2$ と書くこともできますが、より一般化された正射影ベクトルの表記に合わせて、このままにしておきます。
 
正射影ベクトル $\boldsymbol{p}$ は
 \[\boldsymbol{p}=\frac{\boldsymbol{a}^T\boldsymbol{v}}{\boldsymbol{a}^T\boldsymbol{a}}\boldsymbol{a}\tag{3}\]
と表されます。$k$ の求め方さえ知っていれば、いつでも正射影ベクトルをつくることはできますが、$\boldsymbol{v}$ から $\boldsymbol{p}$ への変換行列で表現したほうが線形代数の流儀に沿っています（これは半分冗談です。流儀というだけでなく、この種の変換を部分空間の視点で捉えるためには表現行列は必須です）。

正射影ベクトル $\boldsymbol{p}=k\boldsymbol{a}$ において、$k$ はスカラーなので $\boldsymbol{p}=\boldsymbol{a}k$ と書いても同じことです。すなわち $\boldsymbol{p}$ は
 \[\boldsymbol{p}=\boldsymbol{a}\frac{\boldsymbol{a}^T\boldsymbol{v}}{\boldsymbol{a}^T\boldsymbol{a}}\tag{4}\]
のように書き直せます。さらに、結合法則によって分子は $(\boldsymbol{a}\boldsymbol{a}^T)\boldsymbol{v}$ の順で計算できるので、
 \[\boldsymbol{p}=\frac{\boldsymbol{a}\boldsymbol{a}^T}{\boldsymbol{a}^T\boldsymbol{a}}\boldsymbol{v}\tag{5}\]
のように書くこともできます。線形変換 $P\boldsymbol{v}$ によって正射影ベクトル (3) が得られたと考えるならば、
 \[P=\frac{\boldsymbol{a}\boldsymbol{a}^T}{\boldsymbol{a}^T\boldsymbol{a}}\tag{6}\]
と表されます。$P$ を 射影行列 とよびます。分子と分母は $\boldsymbol{a}$ と $\boldsymbol{a}^{T}$ を掛ける順序が逆になっているだけですが、$\boldsymbol{a}\boldsymbol{a}^T$ は行列、$\boldsymbol{a}^T\boldsymbol{a}$ はスカラーとなります。

たとえば、$\boldsymbol{a}$ が 2 次元ベクトル $\boldsymbol{a}=\begin{bmatrix}a_1\\a_2\end{bmatrix}$ である場合、
 \[\boldsymbol{a}\boldsymbol{a}^T=\begin{bmatrix}a_1\\a_2\end{bmatrix}\begin{bmatrix}a_1&a_2\end{bmatrix}=\begin{bmatrix}a_1^2&a_1a_2\\a_1a_2&a_2^2\end{bmatrix}\tag{7}\]
となります。
 
ここから本質的な話に踏み込んでいきます。正射影ベクトルをつくることは、これまで学んできた 部分空間 への分解そのものです。たとえば、$\boldsymbol{v}$ が $\mathbb{R}^2$ を代表するベクトル $\boldsymbol{v}=\begin{bmatrix}x\\y\end{bmatrix}$ だとすれば、行列 $P$ による線形変換 $P\boldsymbol{v}=\boldsymbol{p}$ は $\mathbb{R}^2$ の列空間 $\mathbb{C}(P)$ であり、$\boldsymbol{p}$ に垂直な $\boldsymbol{v}-\boldsymbol{p}$ は $P$ の左零空間 $\mathrm{Ker}P^T$ となります。
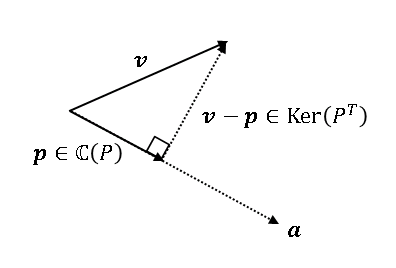 つまり $\mathbb{R}^2$ で正射影ベクトルをつくることは、平面全体をそれぞれの次元が 1 である 2 つの部分空間 (2 本の直線) に分解することを意味します。最も簡単な例をみましょう。$\boldsymbol{v}$ を平面上の任意のベクトル、$\boldsymbol{a}$ を $x$ 軸上の単位ベクトルとします。
 
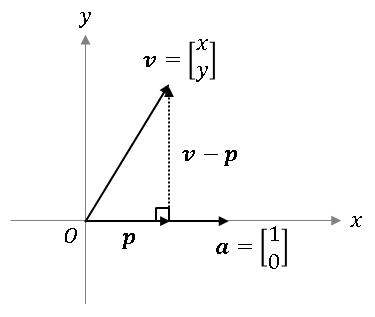
結果は自明なので、馬鹿げていると思うかもしれませんが、敢えて射影行列を使って正射影ベクトルを求めてみます。射影行列は
 \[P=\frac{\boldsymbol{a}\boldsymbol{a}^T}{\boldsymbol{a}^T\boldsymbol{a}}=\boldsymbol{a}\boldsymbol{a}^T=\begin{bmatrix}1\\0\end{bmatrix}\begin{bmatrix}1&0\end{bmatrix}=\begin{bmatrix}1&0\\0&0\end{bmatrix}\tag{8}\]
となるので、
 \[\boldsymbol{p}=P\boldsymbol{v}=\begin{bmatrix}1&0\\0&0\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}x\\0\end{bmatrix}\tag{9}\]
ついでに $\boldsymbol{v}-\boldsymbol{p}$ も求めておきましょう。
 \[\boldsymbol{v}-\boldsymbol{p}=\begin{bmatrix}x\\y\end{bmatrix}-\begin{bmatrix}x\\0\end{bmatrix}=\begin{bmatrix}0\\y\end{bmatrix}\tag{10}\]
射影行列 $P$ によって、$\mathbb{R}^2$ 全体は $x$ 軸と $y$ 軸に分解されました。

平面への正射影

今度は $\mathbb{R}^3$ における線形独立な 2 つのベクトル $\boldsymbol{a}_1,\ \boldsymbol{a}_2$ によって張られる平面への射影について考えます。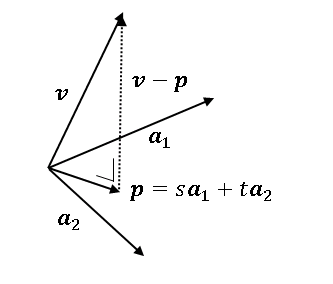基本的な考え方は直線への射影と同じですが、今回は求めるべき変数が 2 つになります。すなわち、$\boldsymbol{a}_1$ と $\boldsymbol{a}_2$ の線形結合
 \[\boldsymbol{p}=s\boldsymbol{a}_1+t\boldsymbol{a}_2\tag{11}\]
がちょうど $\boldsymbol{v}$ の終端の真下にくるように $s$ と $t$ を決定します。$\boldsymbol{p}$ を $\boldsymbol{a}_1,\ \boldsymbol{a}_2$ を横に並べた行列で表すと
 \[\boldsymbol{p}=\begin{bmatrix}\boldsymbol{a}_1&\boldsymbol{a}_2\end{bmatrix}\begin{bmatrix}s\\t\end{bmatrix}\tag{12}\]
となります。ここで行列 $A$ とベクトル $\boldsymbol{x}$ を
 \[A=\begin{bmatrix}\boldsymbol{a}_1&\boldsymbol{a}_2\end{bmatrix},\quad \boldsymbol{x}=\begin{bmatrix}s\\t\end{bmatrix}\]
のように定義すると、$\boldsymbol{p}=A\boldsymbol{x}$ と表せます。

$\boldsymbol{a}_1,\ \boldsymbol{a}_2$ はそれぞれ $\boldsymbol{v}-\boldsymbol{p}$ と垂直 (内積が $0$) なので、
 \[\begin{align*}\boldsymbol{a}_1^T(\boldsymbol{v}-A\boldsymbol{x})=0\tag{13}\\[6pt]\boldsymbol{a}_2^T(\boldsymbol{v}-A\boldsymbol{x})=0\tag{14}\end{align*}\]
が $s$ と $t$ を決定する条件式となります。
 \[A^T=\begin{bmatrix}\boldsymbol{a}_1^T\\\boldsymbol{a}_2^T\end{bmatrix}\tag{15}\]
とおいて行列形式でまとめると、
 \[A^T(\boldsymbol{v}-A\boldsymbol{x})=0\tag{16}\]
となります。少し変形すると
 \[A^TA\boldsymbol{x}=A^T\boldsymbol{v}\tag{17}\]
となります。転置行列の性質 より、$A$ が矩形行列であっても $A^TA$ は常に正方行列です。$A$ を構成するベクトルが線形独立であれば、$\det A\neq 0,\ \det A^T\neq 0$ より、$\det(A^TA)=\det A^T\det A\neq 0$ なので、$A^TA$ には逆行列が存在します。この逆行列を等式 (17) の両辺にかけると
 \[\boldsymbol{x}=(A^TA)^{-1}A^T\boldsymbol{v}\tag{18}\]
が得られます。よって、正射影ベクトルは
 \[\boldsymbol{p}=A\boldsymbol{x}=A(A^TA)^{-1}A^T\boldsymbol{v}\tag{19}\]
で与えられ、$\boldsymbol{v}$ を $\boldsymbol{p}$ に変換する射影行列は
 \[P=A(A^TA)^{-1}A^T\tag{20}\]
で表されます。

$x$ 軸と $y$ 軸に沿う単位ベクトル
 \[\boldsymbol{a}_1=\begin{bmatrix}1\\0\\0\end{bmatrix},\quad\boldsymbol{a}_2=\begin{bmatrix}0\\1\\0\end{bmatrix}\tag{21}\]
によって張られる平面に対する、$\mathbb{R}^3$ のベクトル $\boldsymbol{v}=\begin{bmatrix}x\\y\\z\end{bmatrix}$ の正射影ベクトルを求めてみます。$A$ は $3\times 2$ の矩形行列です。
 \[A=\begin{bmatrix}\boldsymbol{a}_1&\boldsymbol{a}_2\end{bmatrix}=\begin{bmatrix}1&0\\0&1\\0&0\end{bmatrix}\tag{22}\]
射影行列を計算すると $3\times 3$ の正方行列を得ます：
 \[P=A(A^TA)^{-1}A^T=\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix}\tag{23}\]
$\mathbb{R}^3$ のベクトル $\boldsymbol{v}$ に $P$ を作用させると
 \[P\boldsymbol{v}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}x\\y\\0\end{bmatrix}\tag{24}\]
このように、$P$ は $\mathbb{R}^3$ に属する任意のベクトルの $x$ 成分と $y$ 成分を抜き出す行列なので、$P$ の列空間は $xy$ 平面です。$P^T\boldsymbol{v}=\boldsymbol{0}$ を解くと $x=y=0$, $z$ は任意定数となるので、$P$ の左零空間は $z$ 軸です。すなわち、$xy$ 平面と $z$ 軸は $\mathbb{R}^3$ の直交補空間です。

正射影の一般定義

　以上の議論は $\mathbb{R}^n$ 空間における任意次元の部分空間への射影にそのまま適用できます。

すなわち、$\boldsymbol{a}_1,\ \boldsymbol{a}_2,\ \boldsymbol{a}_3…$ によって張られる部分空間に対する正射影ベクトルは、すべての基底ベクトルに垂直になるように決定します。
 \[\begin{align*}\boldsymbol{a}_1^T(\boldsymbol{v}-A\boldsymbol{x})=0\\[6pt]
\boldsymbol{a}_2^T(\boldsymbol{v}-A\boldsymbol{x})=0\\[6pt]
\boldsymbol{a}_3^T(\boldsymbol{v}-A\boldsymbol{x})=0\\[6pt]\cdots\cdots\cdots\cdots\end{align*}\]
$\boldsymbol{a}_1,\ \boldsymbol{a}_2,\ \boldsymbol{a}_3…$ を横に並べた行列を $A$ とおけば、(19) と同じ式
 \[P=A(A^TA)^{-1}A^T\tag{25}\]
を得ることができます。次元が大きくなると、(25) の計算は手間がかかります。SciPy から線形代数ライブラリをインポートして、射影行列を返す関数を定義しましょう。

# python_orthographic_projection

# In[1]

import numpy as np
from scipy import linalg

# 射影行列生成関数
def projection_matrix(x):
    return x @ linalg.inv(x.T @ x) @ x.T

$\mathbb{R}^4$ すなわち 4 次元空間内で、3 つの基底ベクトルによって張られる部分空間への正射影ベクトルを計算してみます。

# In[2]

# 3個の基底ベクトルを並べた行列を定義
A = np.array([[1, 0, 0],
              [0, 1, 0],
              [0, 0, 1],
              [0, 0, 2]])

# Aの射影行列
P = projection_matrix(A)

# 4次元ベクトル
v = np.array([[2, 3, 1, 1]]).T

# ベクトルvの3次元空間への正射影ベクトル
Pv = P @ v

print("射影行列:\n{}\n".format(P))
print("正射影ベクトル:\n{}".format(Pv))

'''
射影行列:
[[1.  0.  0.  0. ]
 [0.  1.  0.  0. ]
 [0.  0.  0.2 0.4]
 [0.  0.  0.4 0.8]]

正射影ベクトル:
[[2. ]
 [3. ]
 [0.6]
 [1.2]]
'''

≫【次の記事】完全正規直交系
≫ Pythonで学ぶ線形代数トップページ