直交補空間

直交補空間

直交部分空間

　『ベクトルの内積』で、ベクトル $\boldsymbol{v}$ と $\boldsymbol{w}$ が直交することを内積を使って $\boldsymbol{v}\cdot\boldsymbol{w}=0$ のように表されることを学びました。今回は部分空間の直交を次のように定義します。

　直交部分空間は、初等幾何学で扱うような「垂直に交わる平面」のような概念とは異なることに注意してください。下図に示すように、$\mathbb{R}^3$ 内の垂直な平面の交線上のベクトルは互いに平行であるので、平面同士は $\mathbb{R}^3$ の直交部分空間ではありません (ただし、四次元空間 $\mathbb{R}^4$ 内の平面であれば事情は異なります)。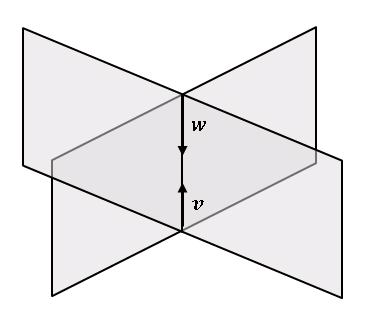

　しかし、$\mathbb{R}^3$ 内の平面と、その平面に直交する直線 (法線) は $\mathbb{R}^3$ の直交部分空間となります。

　ここから本題に入ります。$m\times n$ 行列 $A$ の行空間と核 (零空間) は $\mathbb{R}^n$ の直交部分空間となります。例として $3\times 3$ 行列
　
\[A=\begin{bmatrix}1&1&2\\2&2&4\\1&0&1\end{bmatrix}\tag{1}\]
を考えます。1 行目のベクトルと 2 行目のベクトルが平行なので、この行列の階数は $2$ です ($\mathrm{rank}A=2$)。すなわち、$A$ の行空間 $\mathbb{C}(A^T)$ は 2 つの独立なベクトルによって張られる平面です：
　
\[\mathbb{C}(A^T)=\left\langle\begin{bmatrix}1\\1\\2\end{bmatrix},
\begin{bmatrix}1\\0\\1\end{bmatrix}\right\rangle\tag{2}\]
　核の定義 $A\boldsymbol{x}=\boldsymbol{0}$ は
　
\[\begin{bmatrix}1&1&2\\2&2&4\\1&0&1\end{bmatrix}
\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}0\\0\\0\end{bmatrix}\tag{3}\]
と表せますが、この式は各行ベクトルと $\boldsymbol{x}$ の内積が $0$ であることを意味します。行空間の基底として選んだ 1 行目と 3 行目について書き表すと、
　
\[\begin{bmatrix}1\\1\\2\end{bmatrix}\cdot\boldsymbol{x}=0
,\quad \begin{bmatrix}1\\0\\1\end{bmatrix}\cdot\boldsymbol{x}=0\tag{4}\]
となり、核は行空間の基底に含まれるすべてのベクトルに直交することがわかります。すると、基底ベクトルの線型結合、すなわち行空間の任意のベクトルと核が直交することになります。
　
\[\left\{\alpha\begin{bmatrix}1\\1\\2\end{bmatrix}+\beta\begin{bmatrix}1\\0\\1\end{bmatrix}
\right\}\cdot\boldsymbol{x}=0\tag{5}\]
　すなわち、$A$ の行空間 $\mathbb{C}(A^T)$ と核 $\mathrm{Ker}A$ は $\mathbb{R}^3$ の直交部分空間です。全く同様の議論によって、$A$ の列空間 $\mathbb{C}(A)$ と左零空間 $\mathrm{Ker}A^T$ も $\mathbb{R}^3$ の直交部分空間となります。

　一般に $m\times n$ 行列 $A$ について考えると、行空間 $\mathbb{C}(A^T)$ と核 $\mathrm{Ker}A$ は $\mathbb{R}^n$ の直交部分空間であり、列空間 $\mathbb{C}(A)$ と左零空間 $\mathrm{Ker}A^T$ は $\mathbb{R}^m$ の直交部分空間です。
　

直交補空間

　行空間と核、あるいは列空間と左零空間をペアにする理由は、単に「互いに直交するから」だけではありません。次元の保存が関わってくるからです。前回学んだ公式の一部を再掲します。
　
\[\begin{align*}&\dim\mathbb{C}(A^T)=\mathrm{rank}A\tag{6}\\[6pt]
&\dim(\mathrm{Ker}A)+\mathrm{rank}A=n\tag{7}\end{align*}\]
　(7) は階数・退化次数の定理です。(6), (7) から
　
\[\dim\mathbb{C}(A^T)+\dim(\mathrm{Ker}A)=n\tag{8}\]
を得ます。これは行空間と核が互いに次元を補い合う関係にあることを示しています。$A$ がフルランク ($\mathrm{rank}A=n$) であれば、行空間の次元は $n$, 核の次元は $0$ です。$A$ がランクを $1$ つ落とすごとに行空間の次元は $1$ つ下がり、そのぶんだけ核の次元は増えます (行空間の次元が核へ逃げていくイメージを思い浮かべてください)。同じことは列空間と左零空間の間にも成り立ちますが、次元の和は $A$ の行数 $m$ となります。
　
\[\dim\mathbb{C}(A)+\dim(\mathrm{Ker}A^T)=m\tag{9}\]
　行空間と核、あるいは列空間と左零空間は互いに直交し、次元の和が保存されることがわかりました。これを

のように表現します。線型空間の構造を凝縮した、とても美しい定理です。下図は分解された 4 つの部分空間の関係を表す抽象図です。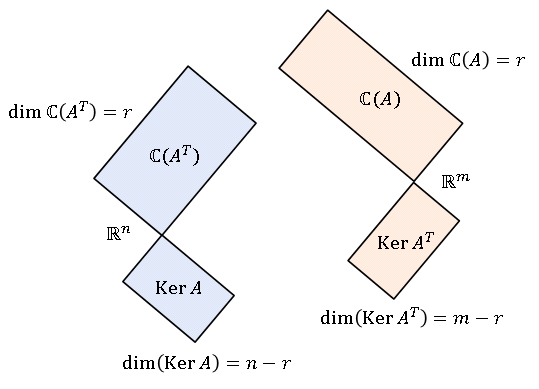

　
　
　任意のベクトル $\boldsymbol{x}$ の行列 $A$ による線型変換 $A\boldsymbol{x}$ を部分空間の視点で眺めてみます。

　行空間に属していようと、核に属していようと、あるいはどちらに属していなくとも、すべてのベクトル $\boldsymbol{x}$ は列空間へと写されます。そのうち核に属するベクトルの写り先が $\boldsymbol{0}$ であることだけは確実です (そういう定義です)。他のベクトルは列空間内の $\boldsymbol{0}$ 以外のどこかに写されます。

　行空間と列空間の関係に焦点を絞ります。
　行空間から $2$ つのベクトル $\boldsymbol{x}_{\,\mathrm{row}},\ \boldsymbol{x}'_{\,\mathrm{row}}$ を選んで $A$ によって変換します。
　このとき、$A\boldsymbol{x}_{\,\mathrm{row}}=A\boldsymbol{x}'_{\,\mathrm{row}}$ を仮定すると、
　
\[A(\boldsymbol{x}_{\,\mathrm{row}}-\boldsymbol{x}'_{\,\mathrm{row}})=\boldsymbol{0}\tag{10}\]
なので、$\boldsymbol{x}_{\,\mathrm{row}}-\boldsymbol{x}'_{\,\mathrm{row}}$ は $A$ の核に属するベクトルとなります。一方で $\boldsymbol{x}_{\,\mathrm{row}}-\boldsymbol{x}'_{\,\mathrm{row}}$ は行空間のベクトル同士の線型結合なので、やはり行空間のベクトルです。行空間と核は直交しているので、両空間に属するベクトルは唯一 $\boldsymbol{0}$ だけです。したがって、
　
\[\boldsymbol{x}_{\,\mathrm{row}}-\boldsymbol{x}'_{\,\mathrm{row}}=\boldsymbol{0}\tag{11}\]
となり、$\boldsymbol{x}_{\,\mathrm{row}}=\boldsymbol{x}'_{\,\mathrm{row}}$ であることがわかります。すなわち、行空間の異なるベクトルは、$A$ によって列空間の異なるベクトルに写されます (行空間から列空間への変換は全単射です)。

　変換 $f$ が集合 $X$ から集合 $Y$ への全単射であるとき、すなわち $Y$ の異なる要素について $X$ の異なる要素が対応するとき、$f$ の逆写像が必ず存在することを思い出してください (『線型写像』を参照)。$A$ が矩形行列であっても、$A\boldsymbol{x}_{\,\mathrm{row}}$ を元の $\boldsymbol{x}_{\,\mathrm{row}}$ に戻すような行列が存在するということです（あくまでも行空間と列空間の間で成り立つ話です）。具体的な表式については「疑似逆行列」の記事で紹介する予定です。