ベクトル空間と部分空間

【Pythonで学ぶ線形代数学講座(13)】ベクトル空間と部分空間
これまでの話を整理すると同時に、もう少し高い視点で線形代数を眺めるために、今回と次回は「ベクトル空間」と「線形写像」という抽象的な概念を解説します。この手の話は知らなくても数値計算で困ることはありませんが、知っておいたほうが「線形代数」の全体像を把握しやすくなると思うので、できれば一読しておいてください。

ベクトル空間

実数成分をもつ 2 次元ベクトルの集合を ${\mathbb{R}}^2$ と記述します。
集合 ${\mathbb{R}}^2$ には 2 次元空間（つまり平面上）のあらゆるベクトルが含まれます。

${\mathbb{R}}^2$ から任意の 2 本のベクトル $\mathit{u},\mathit{v}$ を選んで線形結合
 $$\mathit{w}=\alpha \mathit{u}+\beta \mathit{v}$$
をつくったとき、$\mathit{w}$ もまた集合 ${\mathbb{R}}^2$ の元 (要素) となっています ($\alpha ,\beta$ は実数)。すなわち、${\mathbb{R}}^2$ の元は加算とスカラー倍によって ${\mathbb{R}}^2$ の外に出ることはありません。

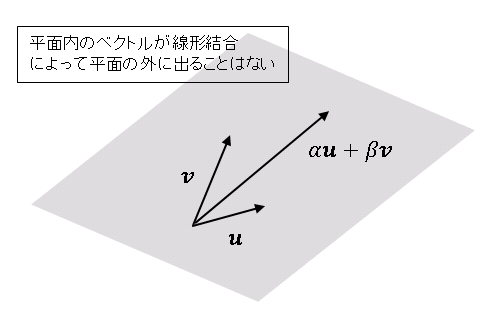
このように、あるベクトル集合 $V$ について、和とスカラー倍の 2 種類の演算が定義され、それらの演算について集合 $V$ が閉じているとき、すなわち
 $$\alpha \mathit{u}+\beta \mathit{v}\in V$$
が成り立つときに、集合 $V$ を ベクトル空間 (vector space) または 線形空間 (linear space) とよびます。厳密にはベクトル空間であるためには以下の 10 個の条件をすべて満たす必要があります。

先に述べた線形結合に関する条件は公理 [1] と[2] をまとめたものです。

非ベクトル空間

平面上の格子点 $\mathit{u}=\left[\begin{array}{c}i\\ j\end{array}\right]$ の集合 $V$ はベクトル空間ではありません ($i,j$ は整数)。
 
和については閉じていますが、スカラー倍については閉じていないからです。
 　
たとえば、ベクトル $\mathit{u}=\left[\begin{array}{c}1\\ 1\end{array}\right]$ にスカラー $0.5$ を掛けると、$\mathit{u}=\left[\begin{array}{c}0.5\\ 0.5\end{array}\right]$ となって、
 
もとの集合からはみ出してしまいます。

n次元ユークリッド空間

$n$ 個の実数を要素にもつベクトルの集合を $n$ 次元ユークリッド空間とよび、${\mathbb{R}}^n$ と書きます。一般には、簡単に $n$ 次元空間とよびます。
 
$\mathbb{R}$ は実数 (Real Number) の頭文字であり、$n$ 個の複素数 (Complex Number) を要素にもつベクトルの集合であれば ${\mathbb{C}}^n$ のように表します。
 
${\mathbb{R}}^1$ は直線、${\mathbb{R}}^2$ は平面、${\mathbb{R}}^3$ は空間を表します。
同様にして $4$ 次元空間 ${\mathbb{R}}^4$、$5$ 次元空間 ${\mathbb{R}}^5$ も定義できます。
 
$n$ 個の要素をもつベクトル同士の線形結合は、$n$ 個の要素をもつベクトルとなるので、${\mathbb{R}}^n$ はベクトル空間です。

行列空間

ベクトル空間は必ずしもベクトルを要素にもつとは限りません。先に挙げた 10 個の公理さえみたせばベクトル空間となりえます。たとえば $2\times 2$ 行列の集合を $\mathbb{M}$ で表せば、$\mathbb{M}$ もまたベクトル空間です。公理を順番にチェックしてみてください。ここでは、[1] と [2] が述べる、要素の線形結合がもとの集合に属していることだけ確認しておきます：
 $$k\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]+l\left[\begin{array}{cc}e& f\\ g& h\end{array}\right]=\left[\begin{array}{cc}ka+lb& kb+lf\\ kc+lg& kd+lh\end{array}\right]$$

関数空間

実数関数 $f(x)$ の集合もベクトル空間です。
対称範囲が広すぎて困惑するかもしれませんが、実数関数 $f(x)$ と $g(x)$ の線形結合 $af(x)+bg(x)$ もやはり実数関数となっていて、他の公理もすべて満たすので、実数関数全体はベクトル空間です (厳密にいえば関数の備えるべき性質にいくらかの条件はつきます)。解析学が絡むので本講座では深入りしませんが、関数は無限個の要素をもつベクトルとして扱えることが知られています。もちろん、もっと範囲を制限した関数の集合をベクトル空間として定義することもできます。その一例として、次節で $2$ 次以下の多項式集合を考えます。

2次以下の多項式の集合

$2$ 次以下の多項式
 $$P=a{x}^2+bx+c$$
の集合 $V$ はベクトル空間です。この集合にはすべての放物線 ($a\ne 0$) と直線 $(a=0,b\ne 0)$、そして点 $(a=b=0)$ が含まれています。$a_1{x}^2+b_{1}x+c_1$ と $a_2{x}^2+b_{2}x+c_2$ の線形結合をつくってみると、
 $$\begin{array}{rl}& \alpha (a_1{x}^2+b_{1}x+c_1)+\beta (a_2{x}^2+b_{2}x+c_2)\\ & =(\alpha a_1+\beta a_2)x^2+(\alpha b_1+\beta b_2)x+(\alpha c_1+\beta c_2)\end{array}$$
となって、$V$ の元であることがわかります。たとえば基底として、
 $${\mathit{e}}_1=x^2,{\mathit{e}}_2=x,{\mathit{e}}_3=1$$
をとれば、ベクトル空間内の任意の点 $\mathit{z}$ を線形結合
 $$\mathit{z}=p{\mathit{e}}_1+q{\mathit{e}}_2+r{\mathit{e}}_3$$
によって表すことができます。これは何も特別なことを表しているわけではありません。2 次式をどのように足し合わせようとも 3 次式にはなれないという当たり前の事実を示しているに過ぎません。$x^2+x$ と $-x^2$ を足すと $x$ になるように、多項式の次数が下がることはありえます。同様に考えて、$n$ 次以下の多項式の集合もベクトル空間であることがわかります。

部分空間

あるベクトル空間 $V$ の中に含まれる、もっと小さなベクトル空間 $S$ を考えることがあります ($S$ が $V$ そのものであってもかまいません)。このとき、$S$ は $V$ の 部分空間 であるといいます。

部分空間 $S$ は慎重に選ぶ必要があります。単に $S$ が $V$ の部分集合となっているだけでは不十分で、ベクトル空間としての要件を満たしていなければなりません。特に ${\mathbb{R}}^n$ のような広い空間が、ほぼ自明として備えていた公理 [5] 、すなわち零元 $\mathbf{0}$ の存在に注意を払う必要があります。

$S$ がベクトル空間であるためには、$S$ に属するベクトル $\mathit{u},\mathit{v}$ について、線形結合 $\alpha \mathit{u}+\beta \mathit{v}$ もまた $S$ に属していなければなりませんが、任意定数を $\alpha =\beta =0$ のように選ぶと、$\mathbf{0}$ となるので、$S$ は最初から $\mathbf{0}$ を含んでいなければなりません。

たとえば、$2$ 次元空間 ${\mathbb{R}}^2$ の部分空間として原点を通る直線を選ぶことはできますが、原点を通らない直線は選べません。原点を通らない直線上の点も ${\mathbb{R}}^2$ に含まれてはいますが、部分空間として採用することはできないのです。原点を通る直線群は ${\mathbb{R}}^2$ の部分空間であると同時に、平面を埋め尽くすので、$V$ に完全一致します。

ベクトル空間の基底と次元

基底については講座の早い段階で学びました。これまでも色々な場面で基底を使ってきましたが、ここであらためて一般化しておきます。

少し難しい表現になってしまいましたが、基底とは空間を張るために過不足のないベクトルの組のことです (多すぎても少なすぎてもいけません)。
 
${\mathbb{R}}^2$ を使って具体的に説明します。
 
${\mathbb{R}}^2$ 内の直交する単位ベクトル $\left[\begin{array}{c}1\\ 0\end{array}\right],\left[\begin{array}{c}0\\ 1\end{array}\right]$ を選んだとします。
 
${\mathbb{R}}^2$、すなわち平面上のすべての点は、この $2$ 本のベクトルの線形結合で表せます。たとえば、$(3,2)$ は
 $$\left[\begin{array}{c}3\\ 2\end{array}\right]=3\left[\begin{array}{c}1\\ 0\end{array}\right]+2\left[\begin{array}{c}0\\ 1\end{array}\right]$$
のように表せます。したがって、$\left[\begin{array}{c}1\\ 0\end{array}\right]$ と $\left[\begin{array}{c}0\\ 1\end{array}\right]$ は ${\mathbb{R}}^2$ の基底となれます。

しかし、$3$ 本目のベクトル $\left[\begin{array}{c}1\\ 1\end{array}\right]$ を加えると、
 $$\left[\begin{array}{c}3\\ 2\end{array}\right]=2\left[\begin{array}{c}1\\ 0\end{array}\right]+\left[\begin{array}{c}0\\ 1\end{array}\right]+\left[\begin{array}{c}1\\ 1\end{array}\right]$$
のように、$(3,2)$ を色々な線形結合で表せるようになってしまいます。
 
$3$ つめは余分なベクトルであって、$\left[\begin{array}{c}1\\ 0\end{array}\right],\left[\begin{array}{c}0\\ 1\end{array}\right],\left[\begin{array}{c}0\\ 1\end{array}\right]$ は基底とはなれません。
 
${\mathbb{R}}^3$ の例を考えてみましょう。$2$ 本のベクトル $\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right],\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$ を選んだとします。
 
これらのベクトルは互いに線形独立ですが、線形結合
 $$a\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]+b\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$$
は平面しか表せないので、${\mathbb{R}}^3$ 全体を表すにはベクトルが不足しています。
 
もう $1$ 本のベクトル $\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$ を加えれば、
 $$a\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]+b\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]+c\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$$
は空間全体を張れるので、${\mathbb{R}}^3$ の基底となれます。
 
一般にベクトル空間 $V$ の基底の取り方は無数にあります。
ベクトル同士が直交している必要もありません。
 
${\mathbb{R}}^2$ であれば、$\left[\begin{array}{c}1\\ 0\end{array}\right],\left[\begin{array}{c}1\\ 1\end{array}\right]$ の代わりに $\left[\begin{array}{c}1\\ 0\end{array}\right],\left[\begin{array}{c}-1\\ 1\end{array}\right]$ を選ぶこともできます。

しかし互いに線形独立であれば、どの組合せをとっても基底に含まれるベクトルの数自体は変わりません。そこで、基底を構成するベクトルの個数をベクトル空間 $V$ の 次元 と定義して $\dim V$ と書きます。
 
たとえば、${\mathbb{R}}^n$ の次元は $n$ なので、$\dim {\mathbb{R}}^n=n$ と表せます。
 
この講座の後半でも扱いますが、微分方程式の解空間も互いに独立な特解 (基底) の線形結合として表せます。たとえば、2階線形微分方程式 $y”+y=0$ の一般解 (解空間) は
 $$y=a\cos x+b\sin x$$
で与えられます。すなわち、$\cos x$ と $\sin x$ が解空間の基底なので次元は $2$ となります。